İkinci dereceden ters matris örneği. Ters matris çevrimiçi

Hizmet amacı. Bu çevrimiçi hizmetin yardımıyla, cebirsel tümleyiciler, transpoze matris AT, adjoint matris ve ters matris bulabilirsiniz.

Cevrimici hesap makinesi. Ters matris.

Çözüm doğrudan web sitesinde (çevrimiçi) gerçekleştirilir ve ücretsizdir. Hesaplama sonuçları bir Word raporunda ve Excel formatında sunulur (yani çözümü kontrol etmek mümkündür). tasarım örneğine bakın.

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Cebirsel tamamlayıcılar.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Sonra ters matrisşu şekilde yazılabilir:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Ters matrisi bulma

А-1 matrisi, А * А-1 = ise, matrise göre ters matris olarak adlandırılır, burada inci mertebenin birim matrisi bulunur. Bir ters matris sadece kare matrisler için var olabilir.

ayrıca bkz. Jordan-Gauss yöntemiyle Ters matris

Ters matrisi bulmak için algoritma

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Transpoze edilmiş matris AT'yi bulma.
Cebirsel tamamlayıcıların tanımı. Matrisin her bir elemanını cebirsel tamamlayıcısı ile değiştirin.
Cebirsel eklemelerden bir ters matris oluşturma: ortaya çıkan matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Ters matrisi bulmak için aşağıdaki algoritma, bazı adımlar dışında bir öncekine benzer: önce cebirsel tamamlayıcılar hesaplanır ve ardından birleşim matrisi belirlenir.

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Cebirsel tamamlayıcıların tanımı.
Birleşim (karşılıklı, ek) matrisinin doldurulması.
Cebirsel tamamlayıcılardan bir ters matris oluşturma: birleşik matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Örnek 1. Matrisi aşağıdaki gibi yazalım:

Matrisin determinantı sıfır değilse bir ters matris vardır. Matrisin determinantını bulun:
= -1 (-1 4 - (- 2 5)) - 2 (2 4 - (- 2 (-2))) + 3 (2 5 - (- 1 (-2))) = 10. Determinant 10 ve sıfıra eşit değildir. Çözüme devam ediyoruz.
Aktarılan matrisi bulun:
Cebirsel tamamlayıcılar.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Sonra ters matrisşu şekilde yazılabilir:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Ters matrisi bulmak için başka bir algoritma

Ters matrisi bulmak için başka bir şema verelim.

Verilen kare matrisin determinantını bulun.
Matrisin tüm elemanlarının cebirsel tamamlayıcılarını bulun.
Satır elemanlarının cebirsel tamamlayıcılarını sütunlara yazarız (transpozisyon).
Elde edilen matrisin her bir elemanını matrisin determinantına böleriz.

Görüldüğü gibi, yer değiştirme işlemi hem başlangıçta orijinal matris üzerinde hem de sonunda elde edilen cebirsel tümleyiciler üzerinde uygulanabilir.

Özel durum: Birim matrisinin tersi, birim matrisidir.

2. Örnek Bir matrisin tersini bulun .
Çözüm.
1. Bul
.
2. A matrisinin her bir elemanının cebirsel tümleyenlerini arıyoruz:
; ; .
İlk satırın elemanlarının cebirsel eklemelerini aldık.

Ters Matrisi Çevrimiçi Bul

Benzer şekilde, ikinci ve üçüncü satırların öğeleri için şunu elde ederiz:
; ; .
; ; .
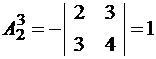3. ve 4. noktaları birleştirerek ters matrisi elde ederiz.

.
Kontrol etmek için A-1A = E olduğundan emin olun.

Talimat. Bir çözüm elde etmek için matrisin boyutunu ayarlamak gerekir. Ardından, yeni bir iletişim kutusunda matrisi doldurun.

Ters matrisi bulma

А-1 matrisi, А * А-1 = ise, matrise göre ters matris olarak adlandırılır, burada inci mertebenin birim matrisi bulunur. Bir ters matris sadece kare matrisler için var olabilir.

Hizmet amacı. Bu çevrimiçi hizmetin yardımıyla, cebirsel tümleyiciler, transpoze matris AT, adjoint matris ve ters matris bulabilirsiniz. Çözüm doğrudan web sitesinde (çevrimiçi) gerçekleştirilir ve ücretsizdir. Hesaplama sonuçları bir Word raporunda ve Excel formatında sunulur (yani çözümü kontrol etmek mümkündür). tasarım örneğine bakın.

Ters matrisi çevrimiçi bulma

ayrıca bkz. Jordan-Gauss yöntemiyle Ters matris

Ters matrisi bulmak için algoritma

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Transpoze edilmiş matris AT'yi bulma.
Cebirsel tamamlayıcıların tanımı. Matrisin her bir elemanını cebirsel tamamlayıcısı ile değiştirin.
Cebirsel eklemelerden bir ters matris oluşturma: ortaya çıkan matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Ters matrisi bulmak için aşağıdaki algoritma, bazı adımlar dışında bir öncekine benzer: önce cebirsel tamamlayıcılar hesaplanır ve ardından birleşim matrisi belirlenir.

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Cebirsel tamamlayıcıların tanımı.
Birleşim (karşılıklı, ek) matrisinin doldurulması.
Cebirsel tamamlayıcılardan bir ters matris oluşturma: birleşik matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Örnek 1. Matrisi aşağıdaki gibi yazalım:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Sonra ters matrisşu şekilde yazılabilir:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Ters matrisi bulmak için başka bir algoritma

Ters matrisi bulmak için başka bir şema verelim.

Verilen kare matrisin determinantını bulun.
Matrisin tüm elemanlarının cebirsel tamamlayıcılarını bulun.
Satır elemanlarının cebirsel tamamlayıcılarını sütunlara yazarız (transpozisyon).
Elde edilen matrisin her bir elemanını matrisin determinantına böleriz.

Görüldüğü gibi, yer değiştirme işlemi hem başlangıçta orijinal matris üzerinde hem de sonunda elde edilen cebirsel tümleyiciler üzerinde uygulanabilir.

Kontrol etmek için A-1A = E olduğundan emin olun.

Talimat. Bir çözüm elde etmek için matrisin boyutunu ayarlamak gerekir. Ardından, yeni bir iletişim kutusunda matrisi doldurun.

Ters matrisi bulmak, lineer cebir bölümünün önemli bir parçasıdır. Bu tür matrislerin yardımıyla, eğer varsa, bir lineer denklem sistemine hızlı bir şekilde bir çözüm bulabilirsiniz.

Aşağıdaki eşitlikler geçerliyse bir matrise matrisin tersi denir.

Bir matrisin determinantı sıfır değilse, matris özellikle değil veya dejenere değil olarak adlandırılır.

Bir matrisin tersi olması için dejenere olmaması gerekli ve yeterlidir.

Ters matrisi bulmak için algoritma

bir kare matrisimiz olsun

ve bunun tam tersini bulmanız gerekir. Bunu yapmak için şu adımları izleyin:

1. Matrisin determinantını bulun. Sıfıra eşit değilse, aşağıdaki işlemleri yaparız. Aksi takdirde, bu matris dejeneredir ve bunun tersi yoktur.

2. Matrisin elemanlarının cebirsel tümleyenlerini bulun. Aradığımız satır ve sütunun toplamının kuvveti ile çarpılan küçüklere eşittirler.

3. Matrisin matrisinin elemanlarının cebirsel tümleyenlerinden bir matris oluşturun ve bunu proto-transpoze edin. Bu matrise bağlı veya müttefik denir ve belirtilir.

4. Ekli matrisi belirleyicilere bölün. Ortaya çıkan matris ters olacak ve makalenin başında açıklanan özelliklere sahip olacaktır.

Matrisin tersini matrisi bulun (Dubovik V.P., Yurik I.I.

Ters matrisi bulma

"Yüksek matematik. Problemlerin toplanması")

1) Matrisin determinantını bulun

Determinant sıfır () olmadığı için ters matris mevcuttur. Cebirsel tamamlayıcılardan oluşan matrisi bulun

Kompleman matrisi şu şekilde olacak

Transpoze ediyoruz ve eki alıyoruz

Bir determinantla böleriz ve tersini alırız

Determinantın bire eşit olduğu durumda, bitişik ve ters matrislerin çakıştığını görüyoruz.

2) Matrisin determinantını hesaplayın

Cebirsel tamamlayıcıların matrisini bulun

Tamamlayıcı matrisin son hali

Bunu devrik ve birleşim matrisini buluyoruz

Ters matrisi bulun

3) Matrisin determinantını hesaplayalım. Bunu yapmak için, ilk satıra genişletin. Sonuç olarak, sıfır olmayan iki terim elde ederiz.

Cebirsel tamamlayıcıların matrisini bulun. Belirleyicinin programı, daha fazla sıfır elemanın (siyah ile işaretlenmiş) olduğu satır ve sütunlarda gerçekleştirilir.

Kompleman matrisinin son hali aşağıdaki gibidir.

Bunu devrik ve ilgili matrisi buluyoruz

Matrisin determinantı bire eşit olduğundan, ters matris bitişik olanla çakışır. Bu örnek geri döndü.

Ters matris hesaplanırken, determinant ve tamamlayıcı matris hesaplanırken yanlış işaretlerle ilişkili hatalar tipiktir.

Daha yüksek matematik »Matrisler ve determinantlar» Ters matris »Cebirsel eklemeler kullanarak ters matrisin hesaplanması.

Cebirsel tamamlayıcıları kullanarak ters matrisi hesaplamak için algoritma: birleşik (birleşik) matris yöntemi.

$ A ^ (- 1) $ matrisi $ A $ kare matrisine göre ters olarak adlandırılır, eğer $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ koşulu sağlanırsa , burada $ E $, sırası $ A $ matrisinin sırasına eşit olan kimlik matrisidir.

Dejenere olmayan matris - determinantı sıfıra eşit olmayan bir matris. Buna göre, dejenere bir matris, determinantın sıfıra eşit olduğu bir matristir.

$ A ^ (- 1) $ ters matrisi, ancak ve ancak $ A $ matrisi dejenere değilse mevcuttur. $ A ^ (- 1) $ ters matrisi varsa, benzersizdir.

Bir matrisin tersini bulmanın birkaç yolu vardır ve biz bunlardan ikisine bakacağız. Bu sayfa, çoğu yüksek matematik dersinde standart olarak kabul edilen birleşik matris yöntemini tartışacaktır. Gauss yönteminin veya Gauss-Jordan yönteminin kullanımını içeren ikinci ters matrisi bulma yöntemi (temel dönüşümler yöntemi) ikinci bölümde tartışılmaktadır.

Birleşik (birleşik) matris yöntemi

$ A_ (n \ çarpı n) $ matrisi verilsin. $ A ^ (- 1) $'ın tersini bulmak için üç adım gereklidir:

$ A $ matrisinin determinantını bulun ve $ \ Delta A \ neq 0 $ olduğundan emin olun, yani. A matrisinin dejenere olmadığı.
$ A $ matrisinin her bir elemanının $ A_ (ij) $ cebirsel tamamlayıcısını oluşturun ve $ A_ (n \ çarpı n) ^ (*) = \ left (A_ (ij) \ right) $ matrisini aşağıdakilerden yazın. cebirsel tamamlayıcılar bulundu.
$ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ formülünü dikkate alarak ters matrisi yazın.

$ (A ^ (*)) ^ T $ matrisi genellikle $ A $ matrisine bitişik (karşılıklı, bitişik) olarak adlandırılır.

Çözüm manuel olarak yapılırsa, ilk yöntem yalnızca nispeten küçük sıralı matrisler için iyidir: ikincisi (örnek No. 2), üçüncüsü (örnek No. 3), dördüncüsü (örnek No. 4). Daha yüksek dereceli bir matrisin tersini bulmak için başka yöntemler kullanılır. Örneğin, ikinci bölümde tartışılan Gauss yöntemi.

Örnek 1

$ A = \ left (\ startup (dizi) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 &'un tersini bulun - 1 & -9 & 0 \ bitiş (dizi) \ sağ) $.

ters matris

Dördüncü sütunun tüm elemanları sıfıra eşit olduğundan, $ \ Delta A = 0 $ (yani $ A $ matrisi dejeneredir). $ \ Delta A = 0 $ olduğundan, $ A $ matrisinin tersi matrisi yoktur.

Örnek 2

$ A = \ sol (\ start (dizi) (cc) -5 & 7 \\ 9 & 8 \ end (dizi) \ sağ) $ matrisinin tersini bulun.

Adjoint matrix yöntemini kullanıyoruz. İlk olarak, verilen $ A $ matrisinin determinantını buluyoruz:

$$ \ Delta A = \ sol | \ start (dizi) (cc) -5 & 7 \\ 9 & 8 \ end (dizi) \ sağ | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

$ \ Delta A \ neq 0 $ olduğundan, ters matris vardır, bu nedenle çözüme devam edeceğiz. Belirli bir matrisin her bir elemanının cebirsel tamamlayıcılarını buluruz:

\ start (hizalanmış) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ bitiş (hizalı)

Cebirsel tamamlayıcılardan bir matris oluşturuyoruz: $ A ^ (*) = \ sol (\ başlangıç (dizi) (cc) 8 & -9 \\ -7 & -5 \ bitiş (dizi) \ sağ) $.

Elde edilen matrisi transpoze edin: $ (A ^ (*)) ^ T = \ sol (\ başlangıç (dizi) (cc) 8 & -7 \\ -9 & -5 \ bitiş (dizi) \ sağ) $ (sonuç matris genellikle $ A $ matrisine bitişik veya birleşik matris olarak adlandırılır). $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ formülünü kullanarak şunları elde ederiz:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ sol (\ başlangıç (dizi) (cc) 8 & -7 \\ -9 & -5 \ bitiş (dizi) \ sağ) = \ sol (\ başlangıç (dizi) (cc) -8/103 ve 7/103 \\ 9/103 ve 5/103 \ bitiş (dizi) \ sağ) $$

Böylece tersi bulunur: $ A ^ (- 1) = \ sol (\ start (dizi) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (dizi) \ sağ) $. Sonucun doğruluğunu kontrol etmek için şu eşitliklerden birinin doğruluğunu kontrol etmek yeterlidir: $ A ^ (- 1) \ cdot A = E $ veya $ A \ cdot A ^ (- 1) = E $. $ A ^ (- 1) \ cdot A = E $ eşitliğini kontrol edelim. Kesirlerle daha az çalışmak için $ A ^ (- 1) $ matrisini $ \ left (\ start (dizi) (cc) -8/103 & 7/103 \\ 9/103 biçiminde değil) ile değiştireceğiz & 5/103 \ end (dizi) \ sağ) $, ve $ - \ frac (1) (103) \ cdot \ sol (\ başlangıç (dizi) (cc) 8 & -7 \\ -9 & -5 olarak \ bitiş (dizi ) \ sağ) $:

Cevap: $ A ^ (- 1) = \ sol (\ başlangıç (dizi) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ bitiş (dizi) \ sağ) $.

Örnek No. 3

$ A = \ sol (\ başlangıç (dizi) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (dizi) \ sağ) $ matrisinin tersini bulun.

$ A $ matrisinin determinantını hesaplayarak başlayalım. Böylece, $ A $ matrisinin determinantı aşağıdaki gibidir:

$$ \ Delta A = \ sol | \ start (dizi) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (dizi) \ sağ | = 18-36 + 56-12 = 26. $$

$ \ Delta A \ neq 0 $ olduğundan, ters matris vardır, bu nedenle çözüme devam edeceğiz. Belirli bir matrisin her bir elemanının cebirsel tamamlayıcılarını buluruz:

Cebirsel tamamlayıcılardan oluşan bir matris oluşturuyoruz ve onu değiştiriyoruz:

$$ A ^ * = \ sol (\ başlangıç (dizi) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ bitiş (dizi) \ sağ); \; (A ^ *) ^ T = \ sol (\ başlangıç (dizi) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ bitiş (dizi) \ sağ) $$

$ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ formülünü kullanarak şunu elde ederiz:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ sol (\ başla (dizi) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (dizi) \ sağ) = \ sol (\ başlangıç (dizi) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ end (dizi) \ sağ) $$

Yani $ A ^ (- 1) = \ sol (\ başlangıç (dizi) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ end (dizi) \ sağ) $. Sonucun doğruluğunu kontrol etmek için şu eşitliklerden birinin doğruluğunu kontrol etmek yeterlidir: $ A ^ (- 1) \ cdot A = E $ veya $ A \ cdot A ^ (- 1) = E $. $ A \ cdot A ^ (- 1) = E $ eşitliğini kontrol edelim. Kesirlerle daha az çalışmak için $ A ^ (- 1) $ matrisini $ \ left (\ startup (dizi) (ccc) 3/13 & -5/26 & 1/26 \ biçiminde değil) ile değiştireceğiz. \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (dizi) \ sağ) $, ve $ \ frac (1) (26) \ cdot \ left ( \ start (dizi) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (dizi) \ sağ) $:

Kontrol başarılı oldu, ters $ A ^ (- 1) $ doğru bulundu.

Cevap: $ A ^ (- 1) = \ sol (\ başlangıç (dizi) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \ end (dizi) \ sağ) $.

Örnek No. 4

$ A = \ left (\ startup (dizi) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8'in tersini bulun & -8 & -3 \ end (dizi) \ sağ) $.

Dördüncü dereceden bir matris için, cebirsel tamamlayıcıları kullanarak ters matrisi bulmak biraz zordur. Ancak, bu tür örnekler test kağıtlarında bulunur.

Bir matrisin tersini bulmak için önce $A $ matrisinin determinantını hesaplamanız gerekir. Bu durumda bunu yapmanın en iyi yolu determinantı satır (sütun) ile genişletmektir. Herhangi bir satırı veya sütunu seçiyoruz ve seçilen satır veya sütunun her bir öğesinin cebirsel tümleyenlerini buluyoruz.

Örneğin, ilk satır için şunu elde ederiz:

$ A $ matrisinin determinantı aşağıdaki formülle hesaplanır:

$$ \ Delta A = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

Cebirsel Tamamlayıcı Matrisi: $ A ^ * = \ sol (\ başlangıç (dizi) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ end (dizi) \ sağ) $.

Birleştirilmiş matris: $ (A ^ *) ^ T = \ sol (\ başla (dizi) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (dizi) \ sağ) $

Ters matris:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ sol (\ başla (dizi) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (dizi) \ sağ) = \ sol (\ başlangıç (dizi) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 & 1/25 & 9/25 & -24/25 \ end (dizi) \ sağ) $$

muayene:

Sonuç olarak, ters matris doğru olarak bulunur.

Cevap: $ A ^ (- 1) = \ sol (\ başlangıç (dizi) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ end (dizi) \ sağ ) $.

İkinci bölümde, Gauss yönteminin veya Gauss-Jordan yönteminin dönüşümlerinin kullanımını içeren ters matrisi bulmanın farklı bir yolu ele alınacaktır.

Yüksek matematikte çevrimiçi dersler

Ters matrisi bulma

А-1 matrisi, А * А-1 = ise, matrise göre ters matris olarak adlandırılır, burada inci mertebenin birim matrisi bulunur. Bir ters matris sadece kare matrisler için var olabilir.

ayrıca bkz. Jordan-Gauss yöntemiyle Ters matris

Ters matrisi bulmak için algoritma

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Transpoze edilmiş matris AT'yi bulma.
Cebirsel tamamlayıcıların tanımı. Matrisin her bir elemanını cebirsel tamamlayıcısı ile değiştirin.
Cebirsel eklemelerden bir ters matris oluşturma: ortaya çıkan matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Ters matrisi bulmak için aşağıdaki algoritma, bazı adımlar dışında bir öncekine benzer: önce cebirsel tamamlayıcılar hesaplanır ve ardından birleşim matrisi belirlenir.

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
Matrisin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Cebirsel tamamlayıcıların tanımı.
Birleşim (karşılıklı, ek) matrisinin doldurulması.
Cebirsel tamamlayıcılardan bir ters matris oluşturma: birleşik matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Örnek 1. Matrisi aşağıdaki gibi yazalım:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Sonra ters matrisşu şekilde yazılabilir:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Ters matrisi bulmak için başka bir algoritma

Ters matrisi bulmak için başka bir şema verelim.

Verilen kare matrisin determinantını bulun.
Matrisin tüm elemanlarının cebirsel tamamlayıcılarını bulun.
Satır elemanlarının cebirsel tamamlayıcılarını sütunlara yazarız (transpozisyon).
Elde edilen matrisin her bir elemanını matrisin determinantına böleriz.

Görüldüğü gibi, yer değiştirme işlemi hem başlangıçta orijinal matris üzerinde hem de sonunda elde edilen cebirsel tümleyiciler üzerinde uygulanabilir.

Kontrol etmek için A-1A = E olduğundan emin olun.

Talimat. Bir çözüm elde etmek için matrisin boyutunu ayarlamak gerekir. Ardından, yeni bir iletişim kutusunda matrisi doldurun.

А -1 matrisi, А * А -1 = Е ise, А matrisine göre ters matris olarak adlandırılır, burada Е, n'inci dereceden birim matristir. Bir ters matris sadece kare matrisler için var olabilir.

Hizmet amacı... Bu çevrimiçi hizmetin yardımıyla cebirsel tümleyiciler, transpoze matris A T, adjoint matris ve ters matris bulabilirsiniz. Çözüm doğrudan web sitesinde (çevrimiçi) gerçekleştirilir ve ücretsizdir. Hesaplama sonuçları bir Word raporunda ve Excel formatında sunulur (yani çözümü kontrol etmek mümkündür). tasarım örneğine bakın.

Talimat. Bir çözüm elde etmek için matrisin boyutunu ayarlamak gerekir. Ardından, yeni bir iletişim kutusunda A matrisini doldurun.

Ayrıca bkz. Jordan-Gauss yöntemini kullanan Ters matris

Ters matrisi bulmak için algoritma

Transpoze edilmiş matris A T'yi bulma.
Cebirsel tamamlayıcıların tanımı. Matrisin her bir elemanını cebirsel tamamlayıcısı ile değiştirin.
Cebirsel eklemelerden bir ters matris oluşturma: ortaya çıkan matrisin her bir elemanı, orijinal matrisin determinantı tarafından bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.

Sonraki ters matris algoritması bazı adımlar dışında bir öncekine benzer: önce cebirsel tamamlayıcılar hesaplanır ve ardından birleşik matris C belirlenir.

Matrisin kare olup olmadığını belirleyin. Değilse, bunun için ters matris yoktur.
A matrisinin determinantının hesaplanması. Sıfıra eşit değilse çözüme devam ederiz, aksi takdirde ters matris yoktur.
Cebirsel tamamlayıcıların tanımı.
Birleşim (karşılıklı, birleşik) matrisinin doldurulması C.
Cebirsel tamamlayıcılardan bir ters matris oluşturma: birleşik matris C'nin her bir elemanı orijinal matrisin determinantına bölünür. Ortaya çıkan matris, orijinal matrisin tersidir.
Bir kontrol yapılır: orijinal ve elde edilen matrisler çarpılır. Sonuç, kimlik matrisi olmalıdır.

Örnek 1. Matrisi aşağıdaki gibi yazalım:

Cebirsel tamamlayıcılar. ∆ 1,2 = - (2 4 - (- 2 (-2))) = -4 ∆ 2,1 = - (2 4-5 3) = 7 ∆ 2,3 = - (- 1 5 - (- 2 2)) = 1 ∆ 3,2 = - (- 1 (-2) -2 3) = 4

bir -1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Ters matrisi bulmak için başka bir algoritma

Ters matrisi bulmak için başka bir şema verelim.

Verilen A kare matrisinin determinantını bulun.
A matrisinin tüm elemanlarının cebirsel tümleyenlerini bulun.
Satır elemanlarının cebirsel tamamlayıcılarını sütunlara yazarız (transpozisyon).
Elde edilen matrisin her bir elemanını A matrisinin determinantına böleriz.

Görüldüğü gibi, yer değiştirme işlemi hem başlangıçta orijinal matris üzerinde hem de sonunda elde edilen cebirsel tümleyiciler üzerinde uygulanabilir.

özel bir durum: E birim matrisinin tersi, E birim matrisidir.

Matrislerle eylemler hakkında konuşmaya devam ediyoruz. Yani - bu ders çalışırken, ters matrisi nasıl bulacağınızı öğreneceksiniz. Öğrenmek. Matematik sıkı olsa bile.

ters matris nedir? Burada karşılıklı sayılarla bir analoji çizebilirsiniz: örneğin, iyimser sayı 5'i ve tersini düşünün. Bu sayıların çarpımı bire eşittir: Matrislerle her şey benzer! Bir matrisin ters matrisi ile çarpımı - kimlik matrisi, sayısal bir birimin matris analogudur. Ancak, her şeyden önce, önemli bir pratik sorunu çözeceğiz, yani bu çok ters matrisi nasıl bulacağımızı öğreneceğiz.

Ters matrisi bulmak için bilmeniz ve yapabilmeniz için neye ihtiyacınız var? karar verebilmelisin belirleyiciler... ne olduğunu anlamalısın matris ve onlarla bazı eylemler gerçekleştirebilir.

Bir matrisin tersini bulmak için iki ana yöntem vardır:
kullanarak cebirsel tamamlayıcılar ve temel dönüşümleri kullanma.

Bugün ilk, daha kolay yolu keşfedeceğiz.

En korkunç ve anlaşılmaz olanla başlayalım. Düşünmek Meydan matris. Ters matris aşağıdaki formülle bulunabilir.:

Matrisin determinantı nerede, matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının transpoze matrisidir.

Ters matris kavramı sadece kare matrisler için vardır., "ikiye iki", "üçe üç" vb. matrisler.

Tanımlamalar: Muhtemelen zaten fark ettiğiniz gibi, matrisin tersi bir üst simge ile gösterilir

En basit durumla başlayalım - ikiye iki matris. Çoğu zaman, elbette, "üçe üç" gereklidir, ancak yine de, çözümün genel ilkesine hakim olmak için daha basit bir görev üzerinde çalışmanızı şiddetle tavsiye ederim.

Örnek:

Bir matrisin tersini bulun

Biz karar veririz. Eylemlerin sırası uygun bir şekilde noktalara bölünebilir.

1) Önce matrisin determinantını bulun.

Bu eylem hakkındaki anlayışınız yeterince iyi değilse, materyali okuyun Determinant nasıl hesaplanır?

Önemli! Matrisin determinantının olması durumunda SIFIR- ters matris BULUNMUYOR.

İncelenen örnekte, ortaya çıktığı gibi, bu, her şeyin yolunda olduğu anlamına gelir.

2) Küçüklerin matrisini bulun.

Sorunumuzu çözmek için reşit olmayanın ne olduğunu bilmek gerekli değildir, ancak makaleyi okumanız önerilir. Determinant nasıl hesaplanır.

Küçüklerin matrisi, matrisle aynı boyutlara sahiptir, yani bu durumda.
Mesele küçük, dört sayı bulmak ve yıldız yerine koymak kalıyor.

Matrisimize geri dön
Önce sol üstteki öğeye bakalım:

nasıl bulunur küçük?
Ve bu şu şekilde yapılır: DÜŞÜNCE bu elemanın bulunduğu satır ve sütunun üzerini çizin:

kalan sayı bu elementin minör, küçük matrisimize yazdığımız:

Aşağıdaki matris öğesini göz önünde bulundurun:

Bu öğenin bulunduğu satırı ve sütunu zihinsel olarak çiziyoruz:

Geriye kalan, matrisimize yazdığımız bu elementin minörüdür:

Benzer şekilde, ikinci satırın unsurlarını ele alır ve küçüklerini buluruz:

Hazır.

Basit. Küçüklerin matrisinde, ihtiyacınız var DEĞİŞİM İŞARETLERİ iki sayı:

Bunlar daire içine aldığım sayılar!

- matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarından oluşan bir matris.

Ve bu sadece...

4) Cebirsel tamamlayıcıların yer değiştiren matrisini bulun.

- matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının transpoze matrisi.

5) Cevap.

Formülümüzü hatırlamak
Her şey bulundu!

Yani matrisin tersi:

Cevap en iyisi olduğu gibi bırakılır. GEREKLİ DEĞİL kesirli sayılar elde ettiğiniz için matrisin her bir öğesini 2'ye bölün. Bu nüans, aynı makalede daha ayrıntılı olarak tartışılmaktadır. matris işlemleri.

Çözümü nasıl kontrol edebilirim?

Matris çarpımı yapmak gereklidir veya

muayene:

Daha önce bahsedilen kimlik matrisiüzerinde olanlar ile bir matris mi ana köşegen ve başka yerlerde sıfırlar.

Dolayısıyla tersi doğrudur.

Bir eylem gerçekleştirirseniz, sonuç aynı zamanda kimlik matrisi olacaktır. Bu, matris çarpımının geçirilebilir olduğu birkaç durumdan biridir, makalede daha fazla bilgi bulunabilir. Matrisler üzerinde işlemlerin özellikleri. matris ifadeleri... Ayrıca, kontrol sırasında sabitin (kesir) öne getirildiğini ve en sonunda - matris çarpımından sonra işlendiğini unutmayın. Bu standart bir tekniktir.

Pratikte daha yaygın bir duruma geçelim - "üçe üç" matrisi:

Örnek:

Bir matrisin tersini bulun

Algoritma, ikiye iki durumla tamamen aynıdır.

Ters matrisi şu formülle buluruz:, matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının transpoze matrisi nerede.

1) Matrisin determinantını bulun.

Burada determinant ortaya çıkıyor ilk satırda.

Ayrıca şunu da unutmayın, bu da her şeyin yolunda olduğu anlamına gelir - ters matris var.

2) Küçüklerin matrisini bulun.

Küçükler matrisi "üçe üç" boyutuna sahiptir ve dokuz sayı bulmamız gerekiyor.

Birkaç küçük ayrıntıya ayrıntılı olarak gireceğim:

Aşağıdaki matris öğesini göz önünde bulundurun:

DÜŞÜNCE bu öğenin bulunduğu satırı ve sütunu çizin:

Kalan dört sayı, "ikiye iki" determinantına yazılır.

Bu niteleyici "ikişer ikişer"dir ve bu elementin minör... Hesaplanması gerekiyor:

İşte bu, minör bulundu, onu minör matrisimize yazıyoruz:

Tahmin edebileceğiniz gibi, hesaplanacak dokuz adet ikiye iki determinant var. Süreç elbette kasvetli, ancak durum en zor değil, daha kötü olabilir.

Peki, pekiştirmek için - resimlerde başka bir küçük bulmak:

Küçüklerin geri kalanını kendiniz hesaplamaya çalışın.

Son sonuç:
- matrisin karşılık gelen elemanlarının küçüklerinin matrisi.

Tüm reşit olmayanların negatif çıkması tamamen tesadüf.

3) Cebirsel tamamlayıcıların matrisini bulun.

Küçüklerin matrisinde, gerekli DEĞİŞİM İŞARETLERİ kesinlikle aşağıdaki unsurlar için:

Bu durumda:

“Dörde dörde” matris için ters matris bulmayı düşünmüyoruz, çünkü böyle bir görev yalnızca sadist bir öğretmen tarafından verilebilir (böylece öğrenci bir belirleyiciyi “dörde dört” ve 16 belirleyiciyi “üçe üç” hesaplar. ). Uygulamamda, böyle bir vakayla karşılaştım ve testin müşterisi işkencemi oldukça pahalıya ödedi =).

Bazı ders kitaplarında, kılavuzlarda, ters matrisi bulmak için biraz farklı bir yaklaşım bulabilirsiniz, ancak yukarıdaki çözüm algoritmasını kullanmanızı öneririm. Niye ya? Çünkü hesaplamalarda ve işaretlerde kafa karıştırma ihtimali çok daha azdır.

Bu konu öğrenciler arasında en nefret edilen konulardan biridir. Sadece belirleyiciler muhtemelen daha kötüdür.

İşin püf noktası, ters eleman kavramının (ve şimdi sadece matrislerden bahsetmiyorum) bizi çarpma işlemine göndermesidir. Okul müfredatında bile çarpma karmaşık bir işlem olarak kabul edilir ve matris çarpımı genellikle ayrı bir konudur, buna bütün bir paragrafı ve eğitim videosunu adadım.

Bugün matris hesaplamalarının detaylarına girmeyeceğiz. Unutmayın: matrisler nasıl gösterilir, nasıl çarpılır ve bundan ne çıkar.

Tekrar: matris çarpımı

Her şeyden önce, notasyon üzerinde anlaşalım. $ A $ boyutunda $ \ left [m \ times n \ right] $ matrisi, yalnızca tam olarak $ m $ satır ve $ n $ sütunun bulunduğu bir sayı tablosudur:

\ = \ destek (\ sol [\ başlangıç (matris) ((a) _ (11))) & ((a) _ (12)) & ... & ((a) _ (1n)) \\ (( a) _ (21) & ((a) _ (22))) & ... & ((a) _ (2n)) \\ ... & ... & ... & ... \\ ((a) _ (m1)) & ((a) _ (m2)) & ... & ((a) _ (mn)) \\\ bitiş (matris) \ sağ]) _ (n) \]

Yer yer satırları ve sütunları yanlışlıkla karıştırmamak için (inanın bana sınavda 1 ile 2'yi karıştırabilirsiniz - oradaki bazı satırlar hakkında ne söyleyebiliriz), resme bir bakmanız yeterli:

Matris hücreleri için indekslerin belirlenmesi

Ne oluyor? Standart koordinat sistemini $ OXY $ sol üst köşeye yerleştirir ve eksenleri tüm matrisi kaplayacak şekilde yönlendirirseniz, bu matrisin her bir hücresi $ \ left (x; y \ sağ) koordinatlarıyla benzersiz bir şekilde ilişkilendirilebilir. $ - bu satır numarası ve sütun numarası olacaktır.

Koordinat sistemi neden sol üst köşede bulunuyor? Çünkü oradan herhangi bir metni okumaya başlıyoruz. Hatırlaması çok kolay.

$ x $ ekseni neden sağa değil de aşağıya doğru yönlendiriliyor? Yine, her şey basit: standart koordinat sistemini alın ($ x $ ekseni sağa gider, $ y $ ekseni yukarı gider) ve matrisi içine alacak şekilde döndürün. Bu, saat yönünde 90 derecelik bir dönüş - sonucunu resimde görebiliriz.

Genel olarak, matris elemanlarının indekslerinin nasıl belirleneceğini bulduk. Şimdi çarpma işlemiyle ilgilenelim.

Tanım. $ A = \ sol [m \ çarpı n \ sağ] $ ve $ B = \ sol [n \ çarpı k \ sağ] $ matrisleri, birincideki sütun sayısı ikincideki satır sayısıyla aynı olduğunda , tutarlı denir.

Bu sırayla. Kafanız karışabilir ve $ A $ ve $ B $ matrislerinin $ \ left (A; B \ right) $ sıralı bir çift oluşturduğunu söylerler: eğer bu sırayla tutarlılarsa, $ B $ ve $ A $, bunlar. $ \ left (B; A \ right) $ çifti de eşleşir.

Yalnızca eşleşen matrisler çarpılabilir.

Tanım. $ A = \ left [m \ times n \ right] $ ve $ B = \ left [n \ times k \ right] $ matrislerinin ürünü yeni bir matris $ C = \ sol [m \ çarpı k \ sağ ] $ , öğeleri $ ((c) _ (ij)) $ aşağıdaki formülle hesaplanır:

\ [((c) _ (ij)) = \ toplam \ limitler_ (k = 1) ^ (n) (((a) _ (ik))) \ cdot ((b) _ (kj)) \]

Başka bir deyişle: $ C = A \ cdot B $ matrisinin $ ((c) _ (ij)) $ öğesini elde etmek için, ilk matrisin $ i $ satırını, $ j $'ı almanız gerekir. ikinci matrisin -th sütununu ve ardından bu satır ve sütundaki öğeleri çiftler halinde çarpın. Sonuçları ekleyin.

Evet, bu çok sert bir tanım. Birkaç gerçek ondan hemen sonra gelir:

Genel olarak konuşursak, matris çarpımı değişmeli değildir: $ A \ cdot B \ ne B \ cdot A $;
Ancak çarpma birleştiricidir: $ \ left (A \ cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ sağ) $;
Ve hatta dağıtımsal olarak: $ \ sol (A + B \ sağ) \ cdot C = A \ cdot C + B \ cdot C $;
Ve yine dağıtımsal olarak: $ A \ cdot \ sol (B + C \ sağ) = A \ cdot B + A \ cdot C $.

Çarpmanın dağılabilirliği, tam da çarpma işleminin değişmeme özelliğinden dolayı, sol ve sağ çarpan toplamı için ayrı ayrı tanımlanmak zorundaydı.

Yine de $ A \ cdot B = B \ cdot A $ olduğu ortaya çıkarsa, bu tür matrislere permütasyon matrisleri denir.

Orada bir şeyle çarpılan tüm matrisler arasında özel olanlar var - herhangi bir $ A $ matrisiyle çarpıldığında tekrar $ A $ verenler:

Tanım. $ A \ cdot E = A $ veya $ E \ cdot A = A $ ise, $ E $ matrisine kimlik denir. $ A $ kare matrisi durumunda şunu yazabiliriz:

Birim matris, matris denklemlerini çözerken sık sık misafir olur. Ve genel olarak, matrisler dünyasına sık sık gelen bir ziyaretçi. :)

Ve ayrıca bu $ E $ yüzünden birisi daha sonra yazılacak olan tüm oyunu ortaya çıkardı.

ters matris nedir

Matris çarpımı çok zaman alan bir işlem olduğundan (bir grup satır ve sütunu çarpmanız gerekir), ters matris kavramı da en önemsiz olanı değildir. Ve biraz açıklama gerektiriyor.

Anahtar tanımı

Pekala, gerçeği öğrenmenin zamanı geldi.

Tanım. $ B $ matrisine, eğer $ A $ matrisinin tersi denir:

Ters matris $ ((A) ^ (- 1)) $ (derece ile karıştırılmamalıdır!) ile gösterilir, yani tanım şu şekilde yeniden yazılabilir:

Görünüşe göre her şey son derece basit ve açık. Ancak böyle bir tanımı analiz ederken, hemen birkaç soru ortaya çıkıyor:

Ters matris her zaman var mıdır? Ve her zaman değilse, o zaman nasıl belirlenir: ne zaman var ve ne zaman yok?
Ve tam olarak böyle bir matris olduğunu kim söyledi? Ya bir başlangıç matrisi $ A $ için tam bir ters matrisler kalabalığı varsa?
Bütün bu terslikler neye benziyor? Ve aslında, nasıl sayılacaklar?

Hesaplama algoritmalarına gelince - bunun hakkında biraz sonra konuşacağız. Ama geri kalan soruları hemen şimdi cevaplayacağız. Bunları ayrı ifadeler-lemmalar şeklinde oluşturalım.

Temel özellikler

$ ((A) ^ (- 1)) $'a sahip olması için $ A $ matrisinin nasıl görünmesi gerektiğiyle başlayalım. Şimdi bu matrislerin her ikisinin de kare ve aynı boyutta olduğundan emin olacağız: $ \ left [n \ times n \ right] $.

Lemma 1. Bir $ A $ matrisi ve bunun tersi $ ((A) ^ (- 1)) $ verildi. O zaman bu matrislerin her ikisi de aynı $ n $ sırasına sahip karedir.

Kanıt. Basit. $ A = \ sol [m \ çarpı n \ sağ] $, $ ((A) ^ (- 1)) = \ sol [a \ çarpı b \ sağ] $ matrisi olsun. $ A \ cdot ((A) ^ (- 1)) = E $ çarpımı tanım olarak mevcut olduğundan, $ A $ ve $ ((A) ^ (- 1)) $ matrisleri belirtilen sırada eşleştirilir:

\ [\ başla (hizala) & \ sol [m \ kez n \ sağ] \ cdot \ sol [a \ kez b \ sağ] = \ sol [m \ kez b \ sağ] \\ & n = a \ bitiş ( hizala) \]

Bu, matris çarpma algoritmasının doğrudan bir sonucudur: $ n $ ve $ a $ katsayıları "geçicidir" ve eşit olmalıdır.

Aynı zamanda, ters çarpma da tanımlanır: $ ((A) ^ (- 1)) \ cdot A = E $, bu nedenle $ ((A) ^ (- 1)) $ ve $ A $ matrisleri ayrıca belirtilen sırayla eşleşir:

\ [\ başlangıç (hizalama) & \ sol [a \ kez b \ sağ] \ cdot \ sol [m \ kez n \ sağ] = \ sol [a \ kez n \ sağ] \\ & b = m \ bitiş ( hizala) \]

Böylece, genelliği kaybetmeden, $ A = \ sol [m \ çarpı n \ sağ] $, $ ((A) ^ (- 1)) = \ sol [n \ çarpı m \ sağ] $ olduğunu varsayabiliriz. Ancak, $ A \ cdot ((A) ^ (- 1)) = ((A) ^ (- 1)) \ cdot A $ tanımına göre matrislerin boyutları kesinlikle aynıdır:

\ [\ başlangıç (hizalama) & \ sol [m \ kez n \ sağ] = \ sol [n \ kez m \ sağ] \\ & m = n \ bitiş (hiza) \]

Böylece, üç matrisin de - $ A $, $ ((A) ^ (- 1)) $ ve $ E $ - kare boyutları $ \ left [n \ çarpı n \ sağ] $ olduğu ortaya çıktı. Lemma kanıtlanmıştır.

Bu zaten kötü değil. Sadece kare matrislerin tersinir olduğunu görüyoruz. Şimdi tersinin her zaman aynı olduğundan emin olalım.

Lemma 2. Bir $ A $ matrisi ve bunun tersi $ ((A) ^ (- 1)) $ verildi. O zaman bu ters tektir.

Kanıt. Tersinden gidelim: $ A $ matrisinin tersinin en az iki kopyası olsun - $ B $ ve $ C $. O halde tanıma göre aşağıdaki eşitlikler doğrudur:

\ [\ başla (hizala) & A \ cdot B = B \ cdot A = E; \\ & A \ cdot C = C \ cdot A = E. \\ \ bitiş (hizalama) \]

Lemma 1'den, dört matrisin de - $ A $, $ B $, $ C $ ve $ E $ - aynı düzenin karesi olduğu sonucuna varıyoruz: $ \ left [n \ çarpı n \ sağ] $. Bu nedenle, ürün tanımlanır:

Matris çarpımı birleştirici (ama değişmeli değil!) olduğundan, şunu yazabiliriz:

\ [\ başla (hizala) & B \ cdot A \ cdot C = \ sol (B \ cdot A \ sağ) \ cdot C = E \ cdot C = C; \\ & B \ cdot A \ cdot C = B \ cdot \ sol (A \ cdot C \ sağ) = B \ cdot E = B; \\ & B \ cdot A \ cdot C = C = B \ Rightarrow B = C. \\ \ bitiş (hizalama) \]

Tek olası seçeneğimiz var: ters matrisin iki kopyası eşittir. Lemma kanıtlanmıştır.

Yukarıdaki akıl yürütme, tüm gerçek sayılar $ b \ ne 0 $ için tersinin benzersizliğinin kanıtını neredeyse kelimesi kelimesine tekrarlar. Tek temel ekleme, matrislerin boyutunu dikkate almaktır.

Bununla birlikte, herhangi bir kare matrisin tersinir olup olmadığı hakkında hala hiçbir şey bilmiyoruz. Burada determinant yardımımıza geliyor - bu, tüm kare matrisler için temel bir özelliktir.

Lemma 3. Size bir $ A $ matrisi verildi. Ters matrisi $ ((A) ^ (- 1)) $ varsa, orijinal matrisin determinantı sıfır değildir:

\ [\ sol | A \ sağ | \ ne 0 \]

Kanıt. $ A $ ve $ ((A) ^ (- 1)) $ öğelerinin $ \ left [n \ times n \ right] $ boyutunda kare matrisler olduğunu zaten biliyoruz. Bu nedenle, her biri için determinantı hesaplayabilirsiniz: $ \ left | A \ sağ | $ ve $ \ sol | ((A) ^ (- 1)) \ sağ | $. Ancak, ürünün determinantı, determinantların ürününe eşittir:

\ [\ sol | A \ cdot B \ sağ | = \ sol | A \ sağ | \ cdot \ sol | B \ sağ | \ Sağ ok \ sol | A \ cdot ((A) ^ (- 1)) \ sağ | = \ sol | A \ sağ | \ cdot \ sol | ((A) ^ (- 1)) \ sağ | \]

Ancak tanıma göre, $ A \ cdot ((A) ^ (- 1)) = E $ ve $ E $'ın determinantı her zaman 1'dir, bu nedenle

\ [\ başla (hizala) & A \ cdot ((A) ^ (- 1)) = E; \\ & \ sol | A \ cdot ((A) ^ (- 1)) \ sağ | = \ sol | E \ sağ |; \\ & \ sol | A \ sağ | \ cdot \ sol | ((A) ^ (- 1)) \ sağ | = 1. \\ \ bitiş (hizalama) \]

İki sayının çarpımı ancak bu sayıların her biri sıfırdan farklıysa bire eşittir:

\ [\ sol | A \ sağ | \ ne 0; \ dörtlü \ sol | ((A) ^ (- 1)) \ sağ | \ ne 0. \]

Böylece $ \ sol | A \ sağ | \ ne 0 $. Lemma kanıtlanmıştır.

Aslında bu gereklilik oldukça mantıklıdır. Şimdi ters matrisi bulmak için algoritmayı analiz edeceğiz - ve sıfır determinantla neden ters matrisin prensipte var olamayacağı oldukça netleşecek.

Ama önce, "yardımcı" bir tanım formüle edelim:

Tanım. Dejenere bir matris, determinantı sıfır olan $ \ left [n \ çarpı n \ sağ] $ boyutunda bir kare matristir.

Böylece her tersinir matrisin dejenere olmadığını söyleyebiliriz.

Bir matrisin tersi nasıl bulunur

Şimdi ters matrisleri bulmak için evrensel bir algoritma ele alacağız. Genel olarak, genel kabul görmüş iki algoritma vardır ve bugün ikincisini de ele alacağız.

Şimdi tartışılacak olan, $ \ left [2 \ times 2 \ right] $ ve - kısmen - $ \ left [3 \ times 3 \ right] $ boyutundaki matrisler için çok verimlidir. Ancak $ \ left [4 \ times 4 \ right] $ boyutundan başlayarak kullanmamak daha iyidir. Neden - şimdi kendin her şeyi anlayacaksın.

cebirsel tamamlayıcılar

Hazırlanmak. Şimdi ağrı olacak. Hayır, merak etmeyin: güzel bir hemşire etekli, bağcıklı çoraplı ve kalçanıza iğne yapmayacaktır. Her şey çok daha sıradan: cebirsel eklemeler ve Majesteleri "Birlik Matrisi" size geliyor.

Ana şeyle başlayalım. Öğeleri $ ((a) _ (ij)) $ olarak adlandırılan $ A = \ sol [n \ çarpı n \ sağ] $ boyutunda bir kare matris olsun. Daha sonra, bu tür her eleman için bir cebirsel tamamlayıcı tanımlanabilir:

Tanım. $ ((A) _ (ij)) $ matrisinin $ i $ -inci satırında ve $ j $ -inci sütununda bulunan $ ((a) _ (ij)) $ öğesine $ ((A) _ (ij)) $ cebirsel tamamlayıcısı sol [n \ kez n \ sağ] $, formun bir yapısıdır

\ [((A) _ (ij)) = ((\ sol (-1 \ sağ)) ^ (i + j)) \ cdot M_ (ij) ^ (*) \]

Burada $ M_ (ij) ^ (*) $, aynı $ i $ -. satır ve $ j $ -th sütununu silerek orijinal $ A $'dan elde edilen matrisin determinantıdır.

Tekrar. $ \ left (i; j \ right) $ koordinatlarına sahip matris öğesinin cebirsel tamamlayıcısı $ ((A) _ (ij)) $ olarak gösterilir ve şemaya göre hesaplanır:

İlk olarak, orijinal matristen $ i $ -satırını ve $j $ -th sütununu silin. Yeni bir kare matris alıyoruz ve determinantını $ M_ (ij) ^ (*) $ olarak gösteriyoruz.
Sonra bu determinantı $ ((\ left (-1 \ right)) ^ (i + j)) $ ile çarpıyoruz - ilk başta bu ifade beyin sıkıcı görünebilir, ama aslında sadece önündeki işareti buluyoruz $ M_ (ij) ^ (*) $.
Sayıyoruz - belirli bir sayı alıyoruz. Onlar. cebirsel tamamlayıcı tam olarak bir sayıdır, yeni bir matris değil, vb.

$ M_ (ij) ^ (*) $ matrisinin kendisine $ ((a) _ (ij)) $ öğesinin tamamlayıcı minörü denir. Ve bu anlamda, cebirsel tamamlayıcının yukarıdaki tanımı, daha karmaşık bir tanımın özel bir durumudur - determinant hakkında derste ele aldığımız şey.

Önemli Not. Genel olarak, "yetişkin" matematiğinde cebirsel eklemeler şu şekilde tanımlanır:

Kare bir matriste $ k $ satır ve $ k $ sütun alıyoruz. Kesişmelerinde, $ \ sol [k \ çarpı k \ sağ] $ boyutunda bir matris elde ederiz - belirleyicisine $ k $ mertebesinin minörü denir ve $ ((M) _ (k)) $ ile gösterilir.

Sonra bu "favoriler" $ k $ satırlarını ve $ k $ sütunlarını siliyoruz. Yine bir kare matris elde ederiz - belirleyicisine tamamlayıcı minör denir ve $ M_ (k) ^ (*) $ ile gösterilir.

$ M_ (k) ^ (*) $ ile $ ((\ sol (-1 \ sağ)) ^ (t)) $ çarpın, burada $ t $ (şimdi dikkat!) Seçilen tüm satırların sayılarının toplamı ve sütunlar... Bu cebirsel toplama olacak.

Üçüncü adıma bir göz atın: aslında 2 bin $ terim toplamı var! Başka bir şey, $ k = 1 $ için sadece 2 terim elde ediyoruz - bunlar aynı $ i + j $ - aradığımız $ ((a) _ (ij)) $ öğesinin "koordinatları" olacak cebirsel tamamlayıcı için.

Bu nedenle, bugün biraz basitleştirilmiş bir tanım kullanıyoruz. Ancak daha sonra göreceğimiz gibi, fazlasıyla yeterli olacaktır. Bundan sonrası çok daha önemli:

Tanım. $ S $ kare matrisi $ A = \ sol [n \ çarpı n \ sağ] $'a bitişik matris, $ A $'dan elde edilen, $ \ sol [n \ çarpı n \ sağ] $ boyutunda yeni bir matristir. $ (( a) _ (ij)) $ cebirsel $ ((A) _ (ij)) $ tamamlayıcısını değiştirerek:

\\ Sağ ok S = \ sol [\ başlangıç (matris) ((A) _ (11))) & ((A) _ (12)) & ... & ((A) _ (1n)) \\ (( A) _ (21) & ((A) _ (22))) & ... & ((A) _ (2n)) \\ ... & ... & ... & ... \\ ((A) _ (n1)) & ((A) _ (n2)) & ... & ((A) _ (nn)) \\\ bitiş (matris) \ sağ] \]

Bu tanımın farkına varıldığı anda akla gelen ilk düşünce, "Bu kadarını saymanız gerekir!" olur. Rahatlayın: saymanız gerekecek, ama çok fazla değil. :)

Peki, bunların hepsi çok güzel, ama neden gerekli? İşte neden.

ana teorem

Biraz geriye gidelim. Lemma 3'te, bir $ A $ tersinir matrisinin her zaman dejenere olmadığı belirtilmişti (yani, determinantı sıfırdan farklı: $ \ left | A \ right | \ ne 0 $).

Yani bunun tersi de doğrudur: $ A $ matrisi dejenere değilse, o zaman her zaman tersinirdir. Ve hatta $ ((A) ^ (- 1)) $ arama şeması bile var. Bunu kontrol et:

Ters matris teoremi. $ A = \ sol [n \ çarpı n \ sağ] $ kare matrisi verilsin ve determinantı sıfırdan farklı olsun: $ \ left | A \ sağ | \ ne 0 $. O zaman $ ((A) ^ (- 1)) $ ters matrisi bulunur ve şu formülle hesaplanır:

\ [((A) ^ (- 1)) = \ frac (1) (\ sol | A \ sağ |) \ cdot ((S) ^ (T)) \]

Ve şimdi - her şey aynı, ancak okunaklı el yazısıyla. Bir matrisin tersini bulmak için şunlara ihtiyacınız vardır:

Determinantı hesapla $ \ left | A \ sağ | $ ve sıfır olmadığından emin olun.
$ S $ birleşim matrisini oluşturun, yani. 100500 cebirsel tamamlayıcı $ ((A) _ (ij)) $'ı sayın ve bunları $ ((a) _ (ij)) $ yerine yerleştirin.
Bu matrisi $ S $ transpoze edin ve sonra onu $ q = (1) / (\ left | A \ right |) \; $ ile çarpın.

Ve bu kadar! $ ((A) ^ (- 1)) $ ters matrisi bulunur. Örneklere bir göz atalım:

\ [\ sol [\ başlangıç (matris) 3 ve 1 \\ 5 ve 2 \\\ bitiş (matris) \ sağ] \]

Çözüm. Şimdi tersinirliği kontrol edelim. Determinantı hesaplayalım:

\ [\ sol | A \ sağ | = \ sol | \ başlangıç (matris) 3 ve 1 \\ 5 ve 2 \\\ bitiş (matris) \ sağ | = 3 \ cdot 2-1 \ cdot 5 = 6-5 = 1 \]

Determinant sıfırdan farklı. Dolayısıyla matris tersinirdir. Birleşim matrisini oluşturalım:

Cebirsel eklemeleri sayalım:

\ [\ başla (hizala) & ((A) _ (11)) = ((\ sol (-1 \ sağ)) ^ (1 + 1)) \ cdot \ sol | 2 \ sağ | = 2; \\ & ((A) _ (12)) = ((\ sol (-1 \ sağ)) ^ (1 + 2)) \ cdot \ sol | 5 \ sağ | = -5; \\ & ((A) _ (21)) = ((\ sol (-1 \ sağ)) ^ (2 + 1)) \ cdot \ sol | 1 \ sağ | = -1; \\ & ((A) _ (22)) = ((\ sol (-1 \ sağ)) ^ (2 + 2)) \ cdot \ sol | 3 \ sağ | = 3. \\ \ bitiş (hizalama) \]

Lütfen dikkat: belirleyiciler | 2 |, | 5 |, | 1 | ve |3 | - bunlar $ \ left [1 \ times 1 \ right] $ boyutundaki matrislerin belirleyicileridir, modüller değil. Onlar. belirleyiciler negatif sayılar içeriyorsa, "eksi"yi çıkarmak gerekli değildir.

Toplamda, birleşim matrisimiz şöyle görünür:

\ [((A) ^ (- 1)) = \ frac (1) (\ sol | A \ sağ |) \ cdot ((S) ^ (T)) = \ frac (1) (1) \ cdot ( (\ sol [\ başlangıç (dizi) (* (35) (r)) 2 & -5 \\ -1 & 3 \\\ end (dizi) \ sağ]) ^ (T)) = \ sol [\ başlangıç (dizi) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (dizi) \ sağ] \]

Hepsi bu kadar. Problem çözüldü.

Cevap. $ \ sol [\ başlangıç (dizi) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (dizi) \ sağ] $

Görev. Matrisin tersini bulun:

\ [\ sol [\ başlangıç (dizi) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ bitiş (dizi) \ sağ] \]

Çözüm. Yine determinantı ele alıyoruz:

\ [\ başla (hizala) & \ sola | \ start (dizi) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (dizi) \ sağ | = \ başlangıç (matris ) \ sol (1 \ cdot 2 \ cdot 1+ \ sol (-1 \ sağ) \ cdot \ sol (-1 \ sağ) \ cdot 1 + 2 \ cdot 0 \ cdot 0 \ sağ) - \\ - \ sol (2 \ cdot 2 \ cdot 1+ \ sol (-1 \ sağ) \ cdot 0 \ cdot 1 + 1 \ cdot \ sol (-1 \ sağ) \ cdot 0 \ sağ) \\\ uç (matris) = \ \ & = \ sol (2 + 1 + 0 \ sağ) - \ sol (4 + 0 + 0 \ sağ) = - 1 \ ne 0. \\ \ bitiş (hizalama) \]

Belirleyici sıfır değil - matris ters çevrilebilir. Ama şimdi en zoru olacak: 9'a kadar (dokuz, lanet olsun!) Cebirsel eklemeler saymanız gerekiyor. Ve her biri $ \ left [2 \ times 2 \ right] $ niteleyicisini içerecektir. uçtu:

\ [\ başlangıç (matris) ((A) _ (11)) = ((\ sol (-1 \ sağ)) ^ (1 + 1)) \ cdot \ sol | \ başlangıç (matris) 2 & -1 \\ 0 & 1 \\\ bitiş (matris) \ sağ | = 2; \\ ((A) _ (12)) = ((\ sol (-1 \ sağ)) ^ (1 + 2)) \ cdot \ sol | \ başlangıç (matris) 0 & -1 \\ 1 & 1 \\\ bitiş (matris) \ sağ | = -1; \\ ((A) _ (13)) = ((\ sol (-1 \ sağ)) ^ (1 + 3)) \ cdot \ sol | \ başlangıç (matris) 0 & 2 \\ 1 & 0 \\\ bitiş (matris) \ sağ | = -2; \\ ... \\ ((A) _ (33)) = ((\ sol (-1 \ sağ)) ^ (3 + 3)) \ cdot \ sol | \ başlangıç (matris) 1 & -1 \\ 0 & 2 \\\ bitiş (matris) \ sağ | = 2; \\ \ bitiş (matris) \]

Kısacası, birleşim matrisi şöyle görünecektir:

Bu nedenle, matrisin tersi şu şekilde olacaktır:

\ [((A) ^ (- 1)) = \ frac (1) (- 1) \ cdot \ sol [\ başlangıç (matris) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\ end (matris) \ sağ] = \ sol [\ başlangıç (dizi) (* (35) (r)) - 2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\ end (dizi) \ sağ] \]

Pekala, hepsi bu. İşte cevap.

Cevap. $ \ sol [\ başlangıç (dizi) (* (35) (r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\ end (dizi) \ sağ ] $

Gördüğünüz gibi, her örneğin sonunda bir kontrol yaptık. Bu bağlamda önemli bir not:

Kontrol etmek için tembel olmayın. Orijinal matrisi bulunan tersi ile çarpın - $ E $ almalısınız.

Bu kontrol, örneğin bir matris denklemini çözerken sonraki hesaplamalarda hata aramaktan çok daha kolay ve hızlıdır.

Alternatif yol

Dediğim gibi, ters matris teoremi $ \ left [2 \ times 2 \ right] $ ve $ \ left [3 \ x 3 \ sağ] $ boyutları için harika çalışıyor (ikinci durumda, o kadar "harika" değil ), Ancak büyük matrisler için üzüntü başlar.

Ancak endişelenmeyin: $ \ left [10 \ x 10 \ right] $ matrisi için bile tersini sakince bulmak için kullanılabilecek alternatif bir algoritma var. Ancak, çoğu zaman olduğu gibi, bu algoritmayı düşünmek için biraz teorik arka plana ihtiyacımız var.

Temel dönüşümler

Matrisin çeşitli dönüşümleri arasında birkaç özel dönüşüm vardır - bunlara temel denir. Tam olarak üç tür dönüşüm vardır:

Çarpma işlemi. $ i $ th satırını (sütun) alabilir ve herhangi bir sayı ile çarpabilirsiniz $ k \ ne 0 $;
Ek. $ i $ inci satıra (sütun) herhangi bir sayı ile çarpılan herhangi bir $ j $ th satır (sütun) ekleyin $ k \ ne 0 $ (elbette yapabilirsiniz ve $ k = 0 $, ama ne anlamı var? Yine de hiçbir şey değişmeyecek).
Yeniden düzenleme. $ i $ th ve $ j $ th satırlarını (sütunları) alın ve değiştirin.

Bu dönüşümlere neden temel deniyor (büyük matrisler için çok basit görünmüyorlar) ve neden sadece üç tane var - bu sorular bugünün dersinin kapsamı dışındadır. Bu nedenle ayrıntılara girmeyeceğiz.

Önemli olan bir şey daha var: Bütün bu sapmaları ekteki matris üzerinde yapmamız gerekiyor. Evet, evet: doğru duydunuz. Şimdi bir tanım daha olacak - bugünün dersinde sonuncusu.

Ekli matris

Elbette okulda denklem sistemlerini toplama yöntemini kullanarak çözdünüz. Peki, bir diziden bir tane daha çıkarın, bazı dizileri bir sayı ile çarpın - hepsi bu.

Yani: şimdi her şey aynı olacak, ama zaten "yetişkin bir şekilde". Hazır?

Tanım. $ A = \ sol [n \ çarpı n \ sağ] $ matrisi ve aynı büyüklükte $ n $ olan $ E $ birim matrisi verilsin. Sonra birleşik matris $ \ left [A \ left | E \ sağ. \ sağ] $, şuna benzeyen yeni bir $ \ left [n \ times 2n \ right] $ matrisidir:

\ [\ sol [A \ sol | E \ sağ. \ sağ] = \ sol [\ başlangıç (dizi) (rrrr | rrrr) ((a) _ (11) & ((a) _ (12)) & ... & ((a) _ (1n)) & 1 & 0 & ... & 0 \\ ((a) _ (21) & ((a) _ (22))) & ... & ((a) _ (2n)) & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... \\ ((a) _ (n1)) & ((a) _ (n2)) & ... & ((a) _ (nn)) & 0 & 0 & ... & 1 \\\ end (dizi) \ sağ] \]

Kısacası, $ A $ matrisini alıyoruz, sağda ona gerekli boyutun $ E $ birim matrisini atadık, güzellik için dikey bir çubukla ayırın - işte bitişik olanı. :)

Amaç ne? İşte ne:

Teorem. $ A $ matrisi ters çevrilebilir olsun. $ \ left [A \ left | E \ sağ. \ sağ] $. kullanılıyorsa temel dize dönüşümleri$ \ left [E \ left | Parlak. \ sağ] $, yani $ A $ 'dan elde edilecek satırları çarparak, çıkararak ve yeniden düzenleyerek, sağdaki $ E $ matrisini, ardından soldan elde edilen $ B $ matrisi $ A $'ın tersidir:

\ [\ sol [A \ sol | E \ sağ. \ sağ] \ ila \ sola [E \ sol | Parlak. \ sağ] \ Sağ Ok B = ((A) ^ (- 1)) \]

Bu kadar basit! Kısacası, ters matrisi bulma algoritması şöyle görünür:

Eklenen $ \ left [A \ left | E \ sağ. \ sağ] $;
$ A $ yerine $ E $ görünene kadar temel dize dönüşümlerini gerçekleştirin;
Tabii ki, solda da bir şey görünecek - bazı matris $ B $. Bu tam tersi olacak;
KÂR! :)

Tabii ki, bunu söylemek yapmaktan çok daha kolay. Şimdi birkaç örneğe bakalım: $ \ left [3 \ kere 3 \ sağ] $ ve $ \ left [4 \ kere 4 \ sağ] $ boyutları için.

Görev. Matrisin tersini bulun:

\ [\ sol [\ başlangıç (dizi) (* (35) (r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\ end (dizi) \ sağ] \ ]

Çözüm. Ekli matrisi oluşturuyoruz:

\ [\ sol [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\ bitiş (dizi) \ sağ] \]

Orijinal matrisin son sütunu birlerle dolu olduğundan, ilk satırı diğerlerinden çıkaralım:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\ bitiş (dizi) \ sağ] \ başlangıç (matris) \ aşağı yön \\ -1 \\ -1 \\\ bitiş (matris) \ ila \\ & \ ila \ sola [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ bitiş (dizi) \ sağ] \\ \ bitiş (hizalama) \]

İlk satır dışında başka kimse yok. Ancak ona dokunmuyoruz, aksi takdirde üçüncü sütunda yeni kaldırılan birimler “çarpmaya” başlayacak.

Ancak ikinci satırı sondan iki kez çıkarabiliriz - sol alt köşede bir tane alırız:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ bitiş (dizi) \ sağ] \ başlangıç (matris) \ \\ \ aşağı ok \\ -2 \\\ bitiş (matris) \ ila \\ & \ sola [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ bitiş (dizi) \ sağ] \\ \ bitiş (hizalama) \]

Şimdi son satırı birinciden ve iki kez ikinciden çıkarabiliriz - bu şekilde ilk sütunu "sıfırlarız":

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (dizi) \ sağ] \ start (matris) -1 \\ -2 \\ \ uparrow \\\ end (matris) \ to \\ & \ to \ sola [\ başla (dizi) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

İkinci satırı -1 ile çarpın ve ardından ilk satırdan 6 kez çıkarın ve sonuncuya 1 kez ekleyin:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (dizi) \ sağ] \ başlangıç (matris) \ \\ \ sol | \ cdot \ sol (-1 \ sağ) \ sağ. \\ \\\ bitiş (matris) \ ila \\ & \ ila \ sola [\ başlangıç (dizi) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (dizi) \ right] \ start (matris) -6 \\ \ updownarrow \\ +1 \\\ end ( matris) \ ila \\ & \ ila \ sola [\ başlangıç (dizi) (rrr | rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \ \ 1 & 0 & 0 & 4 & -7 & 3 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

Geriye kalan tek şey 1. ve 3. satırları değiştirmek:

\ [\ sol [\ başlangıç (dizi) (rrr | rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\ end (dizi) \ sağ] \]

Hazır! Sağda istenen ters matris var.

Cevap. $ \ sol [\ başlangıç (dizi) (* (35) (r)) 4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\ end (dizi) \ sağ ] $

Görev. Matrisin tersini bulun:

\ [\ sol [\ başlangıç (matris) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\ bitiş (matris) \ sağ] \]

Çözüm. Yine, eki oluşturuyoruz:

\ [\ sol [\ başla (dizi) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ bitiş (dizi) \ sağ] \]

Hadi biraz uykumuz gelsin, şimdi ne kadar saymamız gerektiğine üzülelim... ve saymaya başlayalım. İlk olarak, 1. satırı 2. ve 3. satırlardan çıkararak ilk sütunu sıfırlayalım:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (dizi) \ sağ] \ başlangıç (matris) \ aşağı ok \\ -1 \\ -1 \\ \\\ bitiş (matris) \ ila \\ & \ ila \ sola [\ başlangıç (dizi) (rrrr | rrrr) 1 ve 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

2-4. satırlarda çok fazla "eksiler" görüyoruz. Üç satırı da -1 ile çarpın ve ardından 3. satırı diğerlerinden çıkararak üçüncü sütunu kapatın:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \ bitiş (dizi) \ sağ] \ başlangıç (matris) \ \\ \ sol | \ cdot \ sol (-1 \ sağ) \ sağ. \\ \ sol | \ cdot \ sol (-1 \ sağ) \ sağ. \\ \ sol | \ cdot \ sol (-1 \ sağ) \ sağ. \\\ bitiş (matris) \ ila \\ & \ ila \ sola [\ başlangıç (dizi) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \ bitiş (dizi) \ sağ] \ başlangıç (matris) -2 \\ -1 \\ \ updownarrow \\ -2 \\\ end (matris) \ to \\ & \ to \ sola [\ başlangıç (dizi) ( rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

Şimdi orijinal matrisin son sütununu "kızartma" zamanı: 4. satırı diğerlerinden çıkarın:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (dizi ) \ sağ] \ başlangıç (matris) +1 \\ -3 \\ -2 \\ \ uparrow \\\ end (matris) \ to \\ & \ to \ sola [\ başla (dizi) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

Son Rulo: 2. satırı 1. ve 3. satırlardan çıkararak ikinci sütunu kapatın:

\ [\ başla (hizala) & \ sola [\ başla (dizi) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ son ( dizi) \ sağ] \ başlangıç (matris) 6 \\ \ updownarrow \\ -5 \\ \ \\\ end (matris) \ ila \\ & \ ila \ sola [\ başlangıç (dizi) (rrrr | rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (dizi) \ sağ] \\ \ end (hizalama) \]

Ve yine solda birim matris, yani tersi sağda. :)

Cevap. $ \ sol [\ başlangıç (matris) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\ bitiş (matris) \ sağ] $

Hepsi bu kadar. Kendiniz kontrol edin - benim için not edin. :)

Bu yazıda lineer cebirsel denklemler sistemini çözmek için matris yöntemi hakkında konuşacağız, tanımını bulacağız ve çözüm örnekleri vereceğiz.

tanım 1

Ters matris yöntemi bilinmeyenlerin sayısının denklem sayısına eşit olması durumunda bir SLAE'yi çözmek için kullanılan bir yöntemdir.

örnek 1

n bilinmeyenli n lineer denklem sistemine bir çözüm bulun:

11 x 1 + 12 x 2 +. ... ... + bir 1 n x n = b 1 bir n 1 x 1 + bir n 2 x 2 +. ... ... + bir n n x n = b n

Matris kayıt türü : A × X = B

burada A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ bir n 1 bir n 2 ⋯ an n n sistemin matrisidir.

X = x 1 x 2 ⋮ x n - bilinmeyenler sütunu,

B = b 1 b 2 ⋮ b n - serbest katsayılar sütunu.

Elde ettiğimiz denklemden X'i ifade etmeniz gerekiyor. Bunu yapmak için soldaki matris denkleminin her iki tarafını da A - 1 ile çarpmanız gerekir:

A - 1 × A × X = A - 1 × B.

A - 1 × A = E olduğundan, E × X = A - 1 × B veya X = A - 1 × B.

Yorum Yap

A matrisinin ters matrisi, yalnızca d e t A koşulu sıfıra eşit değilse var olma hakkına sahiptir. Bu nedenle, SLAE'yi ters matris yöntemiyle çözerken, her şeyden önce, d e t A.

d e t A sıfıra eşit değilse, sistemin tek bir çözümü vardır: ters matris yöntemini kullanmak. d e t А = 0 ise, sistem bu yöntemle çözülemez.

Ters matris yöntemini kullanarak bir lineer denklem sistemini çözme örneği

Örnek 2

SLAE'yi ters matris yöntemiyle çözüyoruz:

2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2

Nasıl çözülür?

Sistemi A X = B matris denklemi şeklinde yazıyoruz, burada

A = 2 - 4 3 1 - 2 4 3 - 1 5, X = x 1 x 2 x 3, B = 1 3 2.

Bu denklemden X ifade ediyoruz:

A matrisinin determinantını bulun:

det A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25

d e t А 0'a eşit değildir, bu nedenle ters matris çözüm yöntemi bu sistem için uygundur.

Birleşim matrisini kullanarak A - 1 ters matrisini bulun. A i j cebirsel tamamlayıcılarını A matrisinin karşılık gelen elemanlarına hesaplıyoruz:

A 11 = (- 1) (1 + 1) - 2 4 - 1 5 = - 10 + 4 = - 6,

A 12 = (- 1) 1 + 2 1 4 3 5 = - (5 - 12) = 7,

A 13 = (- 1) 1 + 3 1 - 2 3 - 1 = - 1 + 6 = 5,

A 21 = (- 1) 2 + 1 - 4 3 - 1 5 = - (- 20 + 3) = 17,

A 22 = (- 1) 2 + 2 2 3 3 5 - 10 - 9 = 1,

A 23 = (- 1) 2 + 3 2 - 4 3 - 1 = - (- 2 + 12) = - 10,

A 31 = (- 1) 3 + 1 - 4 3 - 2 4 = - 16 + 6 = - 10,

A 32 = (- 1) 3 + 2 2 3 1 4 = - (8 - 3) = - 5,

A 33 = (- 1) 3 + 3 2 - 4 1 - 2 = - 4 + 4 = 0.

A matrisinin cebirsel tamamlayıcılarından oluşan A * birleşim matrisini yazıyoruz:

A * = - 6 7 5 17 1 - 10 - 10 - 5 0

Ters matrisi aşağıdaki formüle göre yazıyoruz:

A - 1 = 1 d e t A (A *) T: A - 1 = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

A - 1 ters matrisini B serbest terimleri sütunu ile çarparız ve sistemin çözümünü elde ederiz:

X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1

Cevap : x 1 = - 1; x 2 = 0; x 3 = 1

Metinde bir hata fark ederseniz, lütfen seçin ve Ctrl + Enter tuşlarına basın