Download lectures on theoretical mechanics. Basic laws and formulas in theoretical mechanics

state autonomous institution

Kaliningrad region

professional educational organization

College of Service and Tourism

A course of lectures with examples practical assignments

"Foundations of Theoretical Mechanics"

by disciplineTechnical mechanics

for students3 course

specialties02/20/04 Fire safety

Kaliningrad

APPROVED

Deputy Director for UR GAU KO VET KSTN. Myasnikova

APPROVED

Methodical Council of GAU KO POO KST

CONSIDERED

At a meeting of the PCC

Editorial team:

Kolganova A.A., methodologist

Falaleeva A.B., teacher of Russian language and literature

Tsvetaeva L.V., chairman of the PCCgeneral mathematical and natural science disciplines

Compiled by:

I.V. Nezvanova teacher of GAU KO VET KST

Content

Dynamics: basic concepts and axioms

Bibliography

Statics: basic concepts and axioms.

Theoretical information

Statics - a section of theoretical mechanics, which considers the properties of forces applied to points solid, and the conditions for their equilibrium. Main goals:

1. Transformations of systems of forces into equivalent systems of forces.

2. Determination of equilibrium conditions for systems of forces acting on a rigid body.

Material point called the simplest model of a material body

any shape, the dimensions of which are small enough and which can be taken as a geometric point with a certain mass. Any set of material points is called a mechanical system. An absolutely solid body is a mechanical system, the distances between the points of which do not change with any interactions.

Force Is a measure of the mechanical interaction of material bodies with each other. Force is a vector quantity, since it is determined by three elements:

numerical value;

direction;

point of application (A).

The unit of measure for force is Newton (N).

Figure 1.1

A system of forces is a combination of forces acting on a body.

A balanced (equal to zero) system of forces is called a system that, being applied to a body, does not change its state.

The system of forces acting on the body can be replaced by one resultant, acting as a system of forces.

Axioms of statics.

Axiom 1: If a balanced system of forces is applied to the body, then it moves uniformly and rectilinearly or is at rest (the law of inertia).

Axiom 2: An absolutely rigid body is in equilibrium under the action of two forces if and only if these forces are equal in magnitude, act in one straight line and are directed in opposite directions. Figure 1.2

Axiom 3: The mechanical state of the body will not be disturbed if a balanced system of forces is added to or subtracted from the system of forces acting on it.

Axiom 4: The resultant of two forces applied to the body is equal to their geometric sum, that is, it is expressed in magnitude and direction by the diagonal of the parallelogram built on these forces as on the sides.

Figure 1.3.

Axiom 5: The forces with which two bodies act on each other are always equal in magnitude and directed along one straight line in opposite directions.

Figure 1.4.

Types of bonds and their reactions

Links any restrictions that impede the movement of a body in space are called. The body, striving under the action of the applied forces to carry out the movement, which is impeded by the connection, will act on it with some force, called force of pressure on communication ... According to the law of equality of action and reaction, the connection will act on the body with the same modulus, but oppositely directed force.
The force with which this connection acts on the body, preventing one or another movement, is called the strength of the reaction (reaction) of the connection .
One of the main provisions of mechanics is bond release principle : any non-free body can be regarded as free if one discards connections and replaces their action with reactions of connections.

The reaction of the connection is directed in the direction opposite to the one where the connection does not allow the body to move. The main types of bonds and their reactions are shown in Table 1.1.

Table 1.1

Types of bonds and their reactions

Communication name

Symbol

Smooth surface (support) - surface (support), friction on which the given body can be neglected.
With free support, the reactionguided perpendicular to the tangent drawn through the pointA body contact1 with support surface2 .

Thread (flexible, non-extensible). The connection, implemented in the form of an inextensible thread, does not allow the body to move away from the suspension point. Therefore, the reaction of the thread is directed along the thread to the point of its suspension.

Weightless rod - a rod, the weight of which can be neglected in comparison with the perceived load.
The reaction of a weightless hinged rectilinear rod is directed along the rod axis.

Movable hinge, hinge-movable support. The reaction is directed along the normal to the support surface.

Rigid termination. In the plane of the rigid termination, there will be two components of the reaction, and the moment of a pair of forceswhich prevents the beam from turning1 relative to pointA .
Rigid fixing in space takes away from body 1 all six degrees of freedom - three displacements along the coordinate axes and three rotations about these axes.
In a spatial rigid termination there will be three components, , and three moments of pairs of forces.

System of converging forces

A system of converging forces is called a system of forces, the lines of action of which intersect at one point. Two forces converging at one point, according to the third axiom of statics, can be replaced by one force -resultant .
The main vector of the system of forces - a value equal to the geometric sum of the forces of the system.

The resultant plane system of converging forces can be determinedgraphically and analytically.

Addition of the system of forces . The addition of a flat system of converging forces is carried out either by successive addition of forces with the construction of an intermediate resultant (Fig. 1.5), or by constructing a force polygon (Fig. 1.6).

Figure 1.5 Figure 1.6

Axis force projection - an algebraic quantity equal to the product of the modulus of the force by the cosine of the angle between the force and the positive direction of the axis.
ProjectionFx(Figure 1.7) axle forces NSpositive if angle α is acute, negative if angle α is obtuse. If the strengthis perpendicular to the axis, then its projection onto the axis is zero.

Figure 1.7

Force projection onto plane Ooh- vector , enclosed between the projections of the beginning and end of the forceonto this plane. Those. the projection of the force onto the plane is a vector quantity, characterized not only by numerical value, but also the direction in the planeOoh (Figure 1.8).

Figure 1.8

Then the projection module on the plane Ooh will be equal to:

Fxy = F cosα,

where α is the angle between the direction of the force and its projection.
An analytical way of setting forces . For an analytical way of setting strengthit is necessary to select a coordinate systemOhyz, in relation to which the direction of the force in space will be determined.
Vector depicting strength, can be plotted if the modulus of this force and the angles α, β, γ, which the force forms with the coordinate axes, are known. PointA force application set separately by its coordinatesNS, at, z... You can set the strength of its projectionsFx, Fy, Fzon the coordinate axes. The modulus of force in this case is determined by the formula:

and the direction cosines are:

, .

Analytical way of adding forces : the projection of the vector of the sum on some axis is equal to the algebraic sum of the projections of the terms of the vectors on the same axis, i.e., if:

then , , .
Knowing Rx, Ry, Rz, we can define the module

and direction cosines:

, , .

Figure 1.9

For the equilibrium of the system of converging forces, it is necessary and sufficient that the resultant of these forces be equal to zero.
1) Geometric equilibrium condition for a converging system of forces : for the equilibrium of the system of converging forces, it is necessary and sufficient that the power polygon built from these forces,

was closed (the end of the vector of the last term

force must be combined with the beginning of the vector of the first term of the force). Then the main vector of the system of forces will be equal to zero ()
2) Analytical Equilibrium Conditions . The modulus of the main vector of the system of forces is determined by the formula. = 0. Insofar as , then the radical expression can be equal to zero only if each term simultaneously vanishes, i.e.

Rx= 0, Ry= 0, R z = 0.

Consequently, for the equilibrium of the spatial system of converging forces, it is necessary and sufficient that the sums of the projections of these forces on each of the three coordinates of the axes be equal to zero:

For the equilibrium of a flat system of converging forces, it is necessary and sufficient that the sums of the projections of the forces on each of the two coordinate axes be equal to zero:

The addition of two parallel forces directed in one direction.

Figure 1.9

Two parallel forces directed in one direction are reduced to one resultant force, parallel to them and directed in the same direction. The magnitude of the resultant is equal to the sum of the magnitudes of these forces, and the point of its application C divides the distance between the lines of action of the forces in an internal way into parts inversely proportional to the magnitudes of these forces, that is

B A C

R = F 1 + F 2

The addition of two unequal parallel forces directed in opposite directions.

Two not equal in magnitude antiparallel forces are reduced to one resultant force parallel to them and directed towards the greater force. The magnitude of the resultant is equal to the difference in the magnitudes of these forces, and the point of its application, C, divides the distance between the lines of action of the forces externally into parts inversely proportional to the magnitudes of these forces, that is

A pair of forces and a moment of force relative to a point.

A moment of power relative to the point O is called, taken with the appropriate sign, the product of the magnitude of the force by the distance h from point O to the line of action of the force ... This product is taken with a plus sign if the strength tends to rotate the body counterclockwise, and with the sign - if the force tends to rotate the body clockwise, that is ... The length of the perpendicular h is calledshoulder of strength point O. Effect of force action i.e. angular acceleration the body is larger, the greater is the magnitude of the moment of force.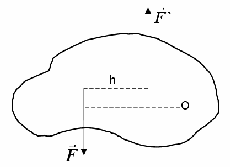

Figure 1.11

With a couple of strengths is called a system consisting of two equal in magnitude parallel forces directed in opposite directions. The distance h between the lines of action of forces is calledshoulder pair . A moment of a couple of forces m (F, F ") is the product of the magnitude of one of the forces that make up the pair on the shoulder of the pair, taken with the appropriate sign.

It is written like this: m (F, F ") = ± F × h, where the product is taken with a plus sign, if a pair of forces tends to rotate the body counterclockwise and with a minus sign, if a pair of forces tends to rotate the body clockwise.

The theorem on the sum of the moments of the forces of a pair.

The sum of the moments of forces of the pair (F, F ") relative to any point 0, taken in the plane of the action of the pair, does not depend on the choice of this point and is equal to the moment of the pair.

Equivalent pair theorem. Consequences.

Theorem. Two pairs, the moments of which are equal to each other, are equivalent, i.e. (F, F ") ~ (P, P")

Corollary 1 ... A pair of forces can be transferred to any place in the plane of its action, as well as rotated at any angle and change the shoulder and the magnitude of the forces of the pair, while maintaining the moment of the pair.

Corollary 2. A pair of forces has no resultant and cannot be balanced by one force lying in the plane of the pair.

Figure 1.12

Addition and equilibrium condition for a system of pairs on a plane.

1. The theorem on the addition of pairs lying in the same plane. A system of pairs, arbitrarily located in the same plane, can be replaced by one pair, the moment of which is equal to the sum moments of these pairs.

2. A theorem on the equilibrium of a system of pairs on a plane.

In order for an absolutely rigid body to be at rest under the action of a system of pairs, arbitrarily located in one plane, it is necessary and sufficient that the sum of the moments of all pairs be equal to zero, that is

The center of gravity

Gravity - the resultant of the forces of attraction to the Earth, distributed over the entire volume of the body.

Body center of gravity - it is such a point invariably connected with this body through which the line of action of the force of gravity of this body passes at any position of the body in space.

Methods for finding the center of gravity

1. Symmetry method:

1.1. If a homogeneous body has a plane of symmetry, then the center of gravity lies in this plane

1.2. If a homogeneous body has an axis of symmetry, then the center of gravity lies on this axis. The center of gravity of a uniform body of revolution lies on the axis of rotation.

1.3 If a homogeneous body has two axes of symmetry, then the center of gravity is at the point of their intersection.

2. Method of splitting: The body is split into the smallest number of parts, the forces of gravity and the position of the centers of gravity of which are known.

3. Method of negative masses: When determining the center of gravity of a body with free cavities, the method of partitioning should be used, but the mass of free cavities should be considered negative.

Coordinates of the center of gravity of a plane figure:

The positions of the centers of gravity of the simple geometric shapes can be calculated using known formulas. (Figure 1.13)

Note: The center of gravity of the symmetry of the figure is on the axis of symmetry.

The center of gravity of the bar is at mid-height.

1.2. Examples of solving practical problems

Example 1: The load is suspended from a rod and is in equilibrium. Determine the efforts in the rod. (figure 1.2.1)

Solution:

The forces arising in the fastening rods are equal in magnitude to the forces with which the rods support the load. (5th axiom)

We determine the possible directions of the reactions of the bonds "rigid rods".

Forces are directed along the rods.

Figure 1.2.1.

Let's free point A from connections, replacing the action of connections with their reactions. (Figure 1.2.2)

We start the construction with a known force by drawing the vectorFon some scale.

From the end of the vectorFdraw lines parallel to reactionsR 1 andR 2 .

Figure 1.2.2

Crossing lines create a triangle. (Figure 1.2.3.). Knowing the scale of the constructions and measuring the length of the sides of the triangle, it is possible to determine the magnitude of the reactions in the rods.

For more accurate calculations, you can use geometric relationships, in particular the theorem of sines: the ratio of the side of a triangle to the sine of the opposite angle is a constant value

For this case:

Figure 1.2.3

Comment: If the direction of the vector (bond reaction) on the given scheme and in the triangle of forces does not coincide, then the reaction on the scheme should be directed in the opposite direction.

Example 2: Determine the magnitude and direction of the resultant flat system of converging forces analytically.

Solution:

Figure 1.2.4

1. Determine the projection of all forces of the system on Ox (Figure 1.2.4)

Adding the projections algebraically, we obtain the projection of the resultant onto the Ox axis.

The sign indicates that the resultant is directed to the left.

2. Determine the projection of all forces on the Oy axis:

Adding the projections algebraically, we obtain the projection of the resultant onto the Oy axis.

The sign indicates that the resultant is directed downward.

3. Determine the modulus of the resultant by the values of the projections:

4. Determine the value of the angle of the resultant with the Ox axis:

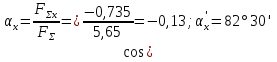
and the value of the angle with the Oy axis:

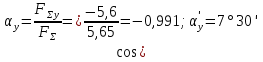
Example 3: Calculate the sum of the moments of forces relative to the point O (Figure 1.2.6).

OA= AB= VD = DE = CB = 2m

Figure 1.2.6

Solution:

1. The moment of force relative to a point is numerically equal to the product of the modulus and the shoulder of the force.

2. The moment of force is equal to zero if the line of action of the force passes through the point.

Example 4: Determine the position of the center of gravity of the figure shown in Figure 1.2.7

Solution:

We split the figure into three:

1-rectangle

A 1 = 10 * 20 = 200cm 2

2-triangle

A 2 = 1/2 * 10 * 15 = 75cm 2

3-circle

A 3 =3,14*3 2 = 28.3cm 2

CG of figure 1: x 1 = 10cm, y 1 = 5cm

CG of figure 2: x 2 = 20 + 1/3 * 15 = 25cm, y 2 = 1/3 * 10 = 3.3cm

CG of figure 3: x 3 = 10cm, y 3 = 5cm

Similarly, y with = 4.5cm

Kinematics: basic concepts.

Basic kinematic parameters

Trajectory - a line outlined by a material point when moving in space. The trajectory can be straight and curved, flat and spatial.

Trajectory equation for plane motion: y =f ( x)

Distance traveled. The path is measured along the path in the direction of travel. Designation -S, units of measurement - meters.

Point motion equation Is an equation that determines the position of a moving point as a function of time.

Figure 2.1

The position of the point at each moment of time can be determined by the distance traveled along the trajectory from some fixed point, considered as the origin (Figure 2.1). This way of setting motion is callednatural ... Thus, the equation of motion can be represented as S = f (t).

Figure 2.2

The position of a point can also be determined if its coordinates are known as a function of time (Figure 2.2). Then, in the case of motion on a plane, two equations must be given:

When spatial movement the third coordinate is addedz= f 3 ( t)

This way of specifying the movement is calledcoordinate .

Travel speed Is a vector quantity that characterizes at the moment the speed and direction of movement along the trajectory.

Velocity is a vector at any moment directed tangentially to the trajectory in the direction of the direction of movement (Figure 2.3).

Figure 2.3

If a point travels equal distances in equal periods of time, then the movement is calleduniform .

Average speed on the path ΔSis determined by:

whereΔS- distance traveled in time Δt; Δ t- time interval.

If a point travels unequal paths in equal intervals of time, then the movement is calleduneven ... In this case, speed is a variable quantity and depends on timev= f( t)

The speed at the moment is defined as

Point acceleration is a vector quantity that characterizes the rate of change in speed in magnitude and direction.

The speed of a point when moving from point M1 to point Mg changes in magnitude and direction. Average acceleration over this period of time

Acceleration at the moment:

Usually, for convenience, two mutually perpendicular components of acceleration are considered: normal and tangential (Figure 2.4)

Normal acceleration a n , characterizes the change in speed along

direction and is defined as

Normal acceleration is always perpendicular to the velocity toward the center of the arc.

Figure 2.4

Tangential acceleration a t , characterizes the change in speed in magnitude and is always directed tangentially to the trajectory; when accelerating, its direction coincides with the direction of the velocity, and when decelerating, it is directed opposite to the direction of the velocity vector.

The full acceleration value is defined as:

Analysis of the types and kinematic parameters of movements

Uniform movement – this movement at a constant speed:

For straight, even motion:

For curved, uniform motion:

The law of uniform motion :

Equivalent motion – this is a motion with a constant tangential acceleration:

For rectilinear equal motion

For curvilinear equal-variable motion:

The law of equal motion:

Kinematic graphs

Kinematic graphs - these are graphs of changes in path, speed and acceleration versus time.

Uniform movement (figure 2.5)

Figure 2.5

Equivalent motion (Figure 2.6)

Figure 2.6

The simplest movements of a rigid body

Translational motion is called the movement of a rigid body, in which any straight line on the body during movement remains parallel to its initial position (Figure 2.7)

Figure 2.7

In translational motion, all points of the body move in the same way: the speeds and accelerations at each moment are the same.

Atrotary motion all points of the body describe a circle around a common fixed axis.

The fixed axis around which all points of the body rotate is calledaxis of rotation.

For description rotary motion bodies around a fixed axis can only be usedangular parameters. (figure 2.8)

φ - the angle of rotation of the body;

ω – angular velocity, determines the change in the angle of rotation per unit of time;

The change in angular velocity over time is determined by the angular acceleration:

2.2. Examples of solving practical problems

Example 1: The equation of motion of a point is given. Determine the speed of the point at the end of the third second of movement and the average speed for the first three seconds.

Solution:

1. Equation of speed

2. Speed at the end of the third second (t=3 c)

3. Average speed

Example 2: According to the given law of motion, determine the type of motion, the initial speed and tangential acceleration of the point, the time to stop.

Solution:

1. Type of movement: equal variable ()
2. When comparing the equations, it is obvious that

- the initial path, traversed before the start of counting 10m;

- initial speed 20m / s

- constant tangential acceleration

- the acceleration is negative, therefore, the movement is slowed down, the acceleration is directed in the direction opposite to the speed of movement.

3. You can define the time at which the speed of the point will be zero.

3.Dynamics: basic concepts and axioms

Dynamics - a section of theoretical mechanics, in which a connection is established between the motion of bodies and the forces acting on them.

Two types of problems are solved in dynamics:

determine the parameters of movement for given forces;

determine the forces acting on the body, according to the given kinematic parameters of motion.

Undermaterial point imply a certain body that has a certain mass (i.e., containing a certain amount of matter), but does not have linear dimensions (an infinitely small volume of space).
Isolated a material point is considered, which is not influenced by other material points. V real world isolated material points, like isolated bodies, do not exist, this concept is conditional.

During translational motion, all points of the body move in the same way, so the body can be taken as a material point.

If the dimensions of the body are small in comparison with the trajectory, it can also be considered as a material point, while the point coincides with the center of gravity of the body.

During the rotational motion of the body, the points may not move in the same way, in this case, some provisions of the dynamics can be applied only to individual points, and the material object can be considered as a set of material points.

Therefore, the dynamics are divided into the dynamics of the point and the dynamics of the material system.

Axioms of dynamics

The first axiom ( principle of inertia): in Any isolated material point is in a state of rest or uniform and rectilinear motion until the applied forces bring it out of this state.

This state is called the stateinertia. Remove the point from this state, i.e. to give her some acceleration, an external force can.

Every body (point) possessesinertia. Body mass is a measure of inertia.

By mass are calledthe amount of substance in the volume of the body, v classical mechanics it is considered a constant value. The unit of measure for mass is kilogram (kg).

Second axiom (Newton's second law is the basic law of dynamics)

F = ma

whereT - point mass, kg;a - point acceleration, m / s 2 .

The acceleration imparted to a material point by force is proportional to the magnitude of the force and coincides with the direction of the force.

Gravity acts on all bodies on Earth, it imparts to the body the acceleration of gravity directed towards the center of the Earth:

G = mg,

whereg - 9.81 m / s², acceleration of gravity.

Third axiom (Newton's third law): csilts of interaction of two bodies are equal in size and directed along one straight line in different directions.

When interacting, accelerations are inversely proportional to masses.

Fourth axiom (the law of independence of the action of forces): toEach force of a system of forces acts as it would act alone.

The acceleration imparted to the point by the system of forces is equal to the geometric sum of the accelerations imparted to the point by each force separately (Figure 3.1):

Figure 3.1

Friction concept. Types of friction.

Friction- resistance arising from the movement of one rough body on the surface of another. When bodies slide, sliding friction occurs, while rolling - swinging friction.

Sliding friction

Figure 3.2.

The reason is the mechanical engagement of the protrusions. The force of resistance to movement during sliding is called the sliding friction force (Figure 3.2)

Sliding friction laws:

1. The sliding friction force is directly proportional to the normal pressure force:

whereR- force of normal pressure, directed perpendicular to the supporting surface;f- coefficient of sliding friction.

Figure 3.3.

In the case of body movement along inclined plane(Figure 3.3)

Rolling friction

Rolling resistance is associated with mutual deformation of the soil and the wheel and is significantly less sliding friction.

For uniform wheel rolling, force must be appliedF dv (Figure 3.4)

The rolling condition of the wheel is that the moving moment must be not less than the moment of resistance:

Figure 3.4.

Example 1: Example 2: To two material points with massm 1 = 2kg andm 2 = 5 kg, the same forces are applied. Compare the values faster.

Solution:

According to the third axiom, acceleration dynamics are inversely proportional to masses:

Example 3: Determine the work of gravity when moving the load from point A to point C along an inclined plane (Figure 3. 7). The force of gravity of the body is 1500N. AB = 6 m, BC = 4m. Example 3: Determine the work of the cutting force in 3 min. Workpiece rotation speed 120 rpm, workpiece diameter 40mm, cutting force 1kN. (Figure 3.8)

Solution:

1. Work in rotary motion:

2. Angular speed 120 rpm

Figure 3.8.

3. The number of revolutions for a given time isz= 120 * 3 = 360 rev.

The angle of rotation during this time is φ = 2πz= 2 * 3.14 * 360 = 2261rad

4. Work in 3 turns:W= 1 * 0.02 * 2261 = 45.2 kJ

Bibliography

Olofinskaya, V.P. "Technical Mechanics", Moscow "Forum" 2011

Erdedi A.A. Erdedi N.A. Theoretical mechanics. Resistance of materials.- Rn-D; Phoenix, 2010

View: this article has been read 32852 times

Pdf Select language ... Russian Ukrainian English

Short review

The entire material is downloaded above, having previously selected the language

Statics
- Basic concepts of statics
- Types of forces
- Axioms of statics
- Connections and their reactions
- System of converging forces
  - Methods for determining the resultant system of converging forces
  - Equilibrium conditions for a system of converging forces
- Moment of force relative to the center as a vector
  - Algebraic magnitude of the moment of force
  - Properties of the moment of force about the center (point)
- The theory of pairs of forces
  - Addition of two parallel forces directed in one direction
  - The addition of two parallel forces directed in opposite directions
  - Couples of forces
  - Pair of forces theorems
  - Equilibrium conditions for a system of pairs of forces
- Lever arm
- Arbitrary flat system of forces
  - Cases of reduction of a plane system of forces to more simple mind
  - Analytical Equilibrium Conditions
- Center of Parallel Forces. The center of gravity
  - Center of Parallel Forces
  - The center of gravity of a rigid body and its coordinates
  - Center of gravity of volume, plane and line
  - Methods for determining the position of the center of gravity
Basics of strength calculations
- Tasks and methods of strength of materials
- Classification of loads
- Classification of structural elements
- Bar deformations
- Basic hypotheses and principles
- Internal forces. Section method
- Voltage
- Stretching and squeezing
- Mechanical characteristics of the material
- Allowable voltages
- Hardness of materials
- Plots of longitudinal forces and stresses
- Shift
- Geometric characteristics of sections
- Torsion
- Bend
  - Differential Bending Constraints
  - Flexural strength
  - Normal voltages. Strength calculation
  - Shear bending stresses
  - Bending stiffness
- The elements general theory stressful condition
- Strength theories
- Torsion bend
Kinematics
- Point kinematics
  - Point trajectory
  - Methods for specifying point movement
  - Point speed
  - Point acceleration
- Rigid body kinematics
  - The translational motion of a rigid body
  - Rotational motion of a rigid body
  - Gear kinematics
  - Plane-parallel movement of a rigid body
- Complex point movement
Dynamics
- Basic laws of dynamics
- Point dynamics
  - Differential Equations free material point
  - Two problems of point dynamics
- Rigid body dynamics
  - Classification of forces acting on a mechanical system
  - Differential equations of motion mechanical system
- General theorems of dynamics
  - The theorem on the motion of the center of mass of a mechanical system
  - Momentum Change Theorem
  - The theorem on the change in the angular momentum
  - The theorem on the change in kinetic energy
Forces acting in machines
- Forces in engagement of a spur gear
- Friction in mechanisms and machines
  - Sliding friction
  - Rolling friction
- Efficiency
Machine parts
- Mechanical transmission
  - Types of mechanical transmissions
  - Basic and derived parameters of mechanical transmissions
  - Gear transmission
  - Flexible link transmissions
- Shafts
  - Purpose and classification
  - Design calculation
  - Check calculation of shafts
- Bearings
  - Plain bearings
  - Rolling bearings
- Connecting machine parts
  - Types of detachable and one-piece connections
  - Keyed connections
Standardization of norms, interchangeability
- Tolerances and landings
- Unified System of Tolerances and Landings (ESDP)
- Geometric Tolerance and Position

Format: pdf

Size: 4MB

Russian language

An example of calculating a spur gear
An example of calculating a spur gear. The choice of material, calculation of permissible stresses, calculation of contact and bending strength were performed.

An example of solving the problem of bending a beam
In the example, diagrams of shear forces and bending moments are constructed, a dangerous section is found and an I-beam is selected. The task analyzed the construction of diagrams using differential dependencies, carried out comparative analysis different cross-sections of the beam.

An example of solving the problem of shaft torsion
The task is to check the strength of a steel shaft for a given diameter, material and allowable stresses. During the solution, diagrams of torques, shear stresses and torsion angles are plotted. The dead weight of the shaft is not taken into account.

An example of solving the problem of tension-compression of a bar
The task is to check the strength of a steel bar at a given allowable stress. In the course of the solution, diagrams of longitudinal forces, normal stresses and displacements are plotted. The self-weight of the bar is not taken into account.

Application of the kinetic energy conservation theorem
An example of solving the problem on the application of the theorem on the conservation of kinetic energy of a mechanical system

Determination of the speed and acceleration of a point according to the given equations of motion
An example of solving a problem to determine the speed and acceleration of a point according to the given equations of motion

Determination of the velocities and accelerations of points of a rigid body during plane-parallel motion
An example of solving the problem of determining the velocities and accelerations of points of a rigid body during plane-parallel motion

Determination of forces in the bars of a flat truss
An example of solving the problem of determining the forces in the bars of a flat truss by the Ritter method and by the method of cutting nodes

Theoretical mechanics- this is a section of mechanics, which sets out the basic laws of mechanical motion and mechanical interaction of material bodies.

Theoretical mechanics is the science in which the movements of bodies over time (mechanical movements) are studied. It serves as the basis for other branches of mechanics (theory of elasticity, resistance of materials, theory of plasticity, theory of mechanisms and machines, hydro-aerodynamics) and many technical disciplines.

Mechanical movement Is change over time mutual position in the space of material bodies.

Mechanical interaction- this is such an interaction as a result of which mechanical movement changes or the relative position of body parts changes.

Rigid body statics

Statics- this is a section of theoretical mechanics, which deals with the problems of equilibrium of rigid bodies and the transformation of one system of forces into another, equivalent to it.

Basic concepts and laws of statics

Absolutely solid(solid, body) is a material body, the distance between any points in which does not change.
Material point Is a body whose dimensions, according to the conditions of the problem, can be neglected.
Free body Is a body, the movement of which is not subject to any restrictions.
Unfree (bound) body Is a body with restrictions imposed on its movement.
Connections- these are bodies that prevent the movement of the object under consideration (body or system of bodies).
Communication reaction Is a force that characterizes the effect of a bond on a rigid body. If we consider the force with which a rigid body acts on a bond as an action, then the bond reaction is a reaction. In this case, the force - the action is applied to the bond, and the bond reaction is applied to the solid.
Mechanical system Is a set of interconnected bodies or material points.
Solid can be considered as a mechanical system, the position and distance between the points of which do not change.
Force Is a vector quantity that characterizes the mechanical action of one material body on another.
Force as a vector is characterized by the point of application, direction of action and absolute value. The unit of measure for the modulus of force is Newton.
Force action line Is a straight line along which the force vector is directed.
Concentrated power- force applied at one point.
Distributed forces (distributed load)- these are the forces acting on all points of the volume, surface or length of the body.
The distributed load is set by the force acting on a unit of volume (surface, length).
The dimension of the distributed load is N / m 3 (N / m 2, N / m).
External force Is a force acting from a body that does not belong to the considered mechanical system.
Inner strength Is a force acting on a material point of a mechanical system from another material point belonging to the system under consideration.
Force system Is a set of forces acting on a mechanical system.
Flat system of forces Is a system of forces, the lines of action of which lie in the same plane.
Spatial system of forces Is a system of forces, the lines of action of which do not lie in the same plane.
System of converging forces Is a system of forces whose lines of action intersect at one point.
Arbitrary system of forces Is a system of forces, the lines of action of which do not intersect at one point.
Equivalent systems of forces- these are systems of forces, the replacement of which one with another does not change the mechanical state of the body.
Accepted designation:.
Equilibrium- this is a state in which the body under the action of forces remains stationary or moves uniformly in a straight line.
Balanced system of forces Is a system of forces that, when applied to a free solid, does not change its mechanical state (does not unbalance).
.
Resultant force Is a force, the action of which on the body is equivalent to the action of the system of forces.
.
Moment of power Is a value that characterizes the rotational ability of a force.
A couple of forces Is a system of two parallel, equal in magnitude, oppositely directed forces.
Accepted designation:.
Under the action of a pair of forces, the body will rotate.
Axis force projection Is a segment enclosed between perpendiculars drawn from the beginning and end of the force vector to this axis.
The projection is positive if the direction of the line segment coincides with the positive direction of the axis.
Force projection onto plane Is a vector on a plane, enclosed between perpendiculars drawn from the beginning and end of the force vector to this plane.
Law 1 (law of inertia). An isolated material point is at rest or moves evenly and rectilinearly.
The uniform and rectilinear motion of a material point is motion by inertia. The state of equilibrium between a material point and a rigid body is understood not only as a state of rest, but also as motion by inertia. For a solid, there are different kinds inertial motion, for example, uniform rotation of a rigid body around a fixed axis.
Law 2. A solid body is in equilibrium under the action of two forces only if these forces are equal in magnitude and directed in opposite directions along the common line of action.
These two forces are called balancing forces.
In general, forces are called balancing if the rigid body to which these forces are applied is at rest.
Law 3. Without disturbing the state (the word "state" here means a state of motion or rest) of a rigid body, one can add and drop counterbalancing forces.
Consequence. Without violating the state of a rigid body, force can be transferred along its line of action to any point in the body.
Two systems of forces are called equivalent if one of them can be replaced by another without violating the state of a rigid body.
Law 4. The resultant of two forces applied at one point, applied at the same point, is equal in magnitude to the diagonal of the parallelogram built on these forces, and is directed along this
diagonals.
The modulus of the resultant is equal to:
Law 5 (the law of equality of action and reaction)... The forces with which two bodies act on each other are equal in magnitude and directed in opposite directions along one straight line.
It should be borne in mind that action- force applied to the body B, and counteraction- force applied to the body A are not balanced, since they are attached to different bodies.
Law 6 (law of hardening)... The equilibrium of a non-solid body is not disturbed when it solidifies.
It should not be forgotten that the conditions of equilibrium, which are necessary and sufficient for a solid, are necessary, but not sufficient for the corresponding non-solid.
Law 7 (the law of release from ties). A non-free rigid body can be considered as free if it is mentally freed from bonds, replacing the action of bonds with the corresponding reactions of bonds.

Connections and their reactions

Smooth surface constrains movement along the normal to the support surface. The reaction is directed perpendicular to the surface.
Articulated movable support constrains the movement of the body along the normal to the reference plane. The reaction is directed along the normal to the support surface.
Articulated fixed support counteracts any movement in a plane perpendicular to the axis of rotation.
Articulated weightless rod counteracts the movement of the body along the line of the bar. The reaction will be directed along the line of the bar.
Blind termination counteracts any movement and rotation in the plane. Its action can be replaced by a force represented in the form of two components and a pair of forces with a moment.

Kinematics

Kinematics- a section of theoretical mechanics that deals with general geometric properties mechanical movement, as a process taking place in space and time. Moving objects are considered as geometric points or geometric bodies.

Basic concepts of kinematics

The law of motion of a point (body) Is the dependence of the position of a point (body) in space on time.
Point trajectory Is the geometrical position of a point in space during its movement.
Point (body) speed- This is a characteristic of the change in time of the position of a point (body) in space.
Point (body) acceleration- This is a characteristic of the change in time of the speed of a point (body).

Determination of kinematic characteristics of a point

Point trajectory
In the vector frame of reference, the trajectory is described by the expression:.
In the coordinate system of reference, the trajectory is determined according to the law of motion of a point and is described by the expressions z = f (x, y)- in space, or y = f (x)- in the plane.
In the natural frame of reference, the trajectory is set in advance.
Determining the speed of a point in a vector coordinate system
When specifying the movement of a point in a vector coordinate system, the ratio of the movement to the time interval is called the average value of the speed in this time interval:.
Taking the time interval as an infinitely small value, the speed value is obtained at a given time (instantaneous speed value): .
The average velocity vector is directed along the vector in the direction of the point's movement, the instantaneous velocity vector is directed tangentially to the trajectory in the direction of the point's movement.
Output: the speed of a point is a vector quantity equal to the derivative of the law of motion with respect to time.
Derivative property: the derivative of any quantity with respect to time determines the rate of change of this quantity.
Determining the speed of a point in a coordinate system
Point coordinates change rates:
.
The modulus of the full speed of a point with a rectangular coordinate system will be equal to:
.
The direction of the velocity vector is determined by the cosines of the direction angles:
,
where are the angles between the velocity vector and the coordinate axes.
Determining the speed of a point in the natural frame of reference
The speed of a point in the natural frame of reference is determined as a derivative of the law of motion of a point:.
According to the previous conclusions, the velocity vector is directed tangentially to the trajectory in the direction of movement of the point and in the axes is determined by only one projection.

Rigid body kinematics

In the kinematics of solids, two main tasks are solved:
1) the task of movement and the determination of the kinematic characteristics of the body as a whole;
2) determination of the kinematic characteristics of the points of the body.
The translational motion of a rigid body
Translational movement is a movement in which a straight line drawn through two points of the body remains parallel to its original position.
Theorem: during translational motion, all points of the body move along the same trajectories and at each moment of time have the same velocity and acceleration in magnitude and direction.
Output: the translational movement of a rigid body is determined by the movement of any of its points, and therefore, the task and study of its movement is reduced to the kinematics of the point.
Rotational movement of a rigid body around a fixed axis
The rotational movement of a rigid body around a fixed axis is the movement of a rigid body in which two points belonging to the body remain motionless during the entire time of movement.
The position of the body is determined by the angle of rotation. The angle unit is radians. (Radian is the central angle of a circle whose arc length is equal to the radius, the total angle of the circle contains 2π radians.)
The law of rotational motion of a body around a fixed axis.
The angular velocity and angular acceleration of the body is determined by the differentiation method:
- angular velocity, rad / s;
- angular acceleration, rad / s².
If you cut the body with a plane perpendicular to the axis, select the point on the axis of rotation WITH and an arbitrary point M then point M will describe around the point WITH circle radius R... During dt an elementary rotation through an angle occurs, while the point M will move along the trajectory at a distance .
Linear speed module:
.
Point acceleration M with a known trajectory, it is determined by its components:
,
where .
As a result, we get the formulas
tangential acceleration: ;
normal acceleration: .

Dynamics

Dynamics- This is a section of theoretical mechanics in which the mechanical movements of material bodies are studied, depending on the reasons that cause them.

Basic concepts of dynamics

Inertia- this is the property of material bodies to maintain a state of rest or uniform rectilinear motion until external forces change this state.
Weight Is a quantitative measure of body inertia. The unit of measure for mass is kilogram (kg).
Material point Is a body with a mass, the dimensions of which are neglected when solving this problem.
Center of gravity of the mechanical system — geometric point, the coordinates of which are determined by the formulas:

where m k, x k, y k, z k- mass and coordinates k-th point of the mechanical system, m Is the mass of the system.
In a homogeneous gravity field, the position of the center of mass coincides with the position of the center of gravity.
Moment of inertia of a material body about the axis Is a quantitative measure of rotational inertia.
The moment of inertia of a material point about the axis is equal to the product of the point's mass by the square of the point's distance from the axis:
.
The moment of inertia of the system (body) about the axis is equal to the arithmetic sum of the moments of inertia of all points:
The force of inertia of a material point Is a vector quantity equal in magnitude to the product of the point mass by the acceleration modulus and directed opposite to the acceleration vector:
The force of inertia of a material body Is a vector quantity equal in modulus to the product of the body mass by the modulus of acceleration of the center of mass of the body and directed opposite to the vector of acceleration of the center of mass:,
where is the acceleration of the center of mass of the body.
Elementary Force Impulse Is a vector quantity equal to the product of the force vector by an infinitely small time interval dt:
.
The total impulse of force for Δt is equal to the integral of elementary impulses:
.
Elementary work of strength Is a scalar dA equal to the scalar proi

Lectures on theoretical mechanics

Point dynamics

Lecture 1

Basic concepts of dynamics

In chapter Dynamics the movement of bodies under the action of forces applied to them is studied. Therefore, in addition to the concepts that were introduced in the section Kinematics, here it is necessary to use new concepts that reflect the specifics of the effect of forces on various bodies and the reaction of bodies to these influences. Let's consider the main of these concepts.

a) strength

Force is a quantitative result of the impact on a given body from other bodies. Force is a vector quantity (Fig. 1).

Point A of the beginning of the force vector F called point of application of force... The straight line MN on which the force vector is located is called line of action of force. The length of a force vector, measured on a certain scale, is called numerical value or modulus of the force vector... The force modulus is denoted as or. The action of the force on the body is manifested either in its deformation, if the body is motionless, or in imparting acceleration to it when the body moves. On these manifestations of force, the device of various devices (force meters or dynamometers) for measuring forces is based.

b) system of forces

The set of forces under consideration forms system of forces. Any system consisting of n forces can be written in the following form:

c) free body

A body that can move in space in any direction without experiencing direct (mechanical) interaction with other bodies is called free or isolated... The effect of one or another system of forces on a body can be clarified only if this body is free.

d) resultant force

If any force exerts the same effect on a free body as a certain system of forces, then this force is called the resultant of this system of forces... This is written as follows:

which means equivalence action on one and the same free body of the resultant and some system of n forces.

Let us now proceed to consider more complex concepts related to the quantitative determination of the rotational effects of forces.

e) moment of force about a point (center)

If the body under the action of force can rotate around some fixed point O (Fig. 2), then to quantify this rotational effect, a physical quantity is introduced, which is called moment of force about a point (center).

The plane passing through a given fixed point and the line of action of the force is called plane of action of force... In Fig. 2, this is the plane ОАВ.

The moment of force relative to a point (center) is a vector quantity equal to the vector product of the radius vector of the point of application of the force by the force vector:

( 1)

According to the rule of vector multiplication of two vectors, their vector product is a vector perpendicular to the plane of location of the vectors of the factors (in this case, the plane of the triangle OAB), directed in the direction from which the shortest rotation of the first vector of the factor to the second vector is visible against the clock hand (Fig. 2). With this order of the vectors of the factors of the vector product (1), the rotation of the body under the action of the force will be visible against the clock hand (Fig. 2) Since the vector is perpendicular to the plane of action of the force, its location in space determines the position of the plane of action of the force. relative to the center is equal to the doubled area ОАВ and can be determined by the formula:

, (2)

where magnitudeh, equal to the shortest distance from a given point O to the line of action of the force, is called the shoulder of the force.

If the position of the plane of action of the force in space is not essential for the characteristic of the rotational action of the force, then in this case, to characterize the rotational action of the force, instead of the vector of the moment of force is used algebraic moment of force:

(3)

The algebraic moment of force relative to a given center is equal to the product of the modulus of force by its shoulder, taken with a plus or minus sign. In this case, the positive moment corresponds to the rotation of the body under the action of the given force against the clock hand, and the negative moment corresponds to the rotation of the body along the clock hand. From formulas (1), (2) and (3) it follows that the moment of force relative to the point is zero only if the shoulder of this forcehequal to zero... Such a force cannot rotate the body around a given point.

f) Moment of force about the axis

If the body under the action of force can rotate around some fixed axis (for example, the rotation of a door or window frame in hinges when they are opened or closed), then to quantify this rotational effect, a physical quantity is introduced, which is called moment of force about a given axis.

 b F xy

Figure 3 shows a diagram in accordance with which the moment of force relative to the z axis is determined:

The angle  is formed by two perpendicular directions z and to the planes of triangles O ab and OAV, respectively. Since  O ab is the projection of ОАВ onto the xy plane, then by the stereometry theorem on the projection of a plane figure onto this plane we have:

where the plus sign corresponds to the positive value of cos, i.e. acute angles , and the minus sign corresponds to the negative value of cos, i.e. to obtuse angles , which is due to the direction of the vector. In turn, SO ab=1/2abh, where h  ab ... Segment size ab is equal to the projection of the force on the xy plane, i.e. . ab = F xy .

Based on the above, as well as equalities (4) and (5), we define the moment of force relative to the z axis as follows:

Equality (6) allows us to formulate the following definition of the moment of force relative to any axis: The moment of force relative to a given axis is equal to the projection on this axis of the vector of the moment of this force relative to any point of this axis and is defined as the product of the projection of the force on the plane perpendicular to this axis, taken with a plus or minus sign on the shoulder of this projection relative to the point of intersection of the axis with the projection plane. In this case, the sign of the moment is considered positive if, looking from the positive direction of the axis, the rotation of the body around this axis is visible against the clock hand. Otherwise, the moment of force about the axis is taken negative. Since this definition of the moment of force about the axis is rather difficult to memorize, it is recommended to remember the formula (6) and Fig. 3, which explains this formula.

From formula (6) it follows that the moment of force about the axis is zero if it is parallel to the axis (in this case, its projection onto a plane perpendicular to the axis is zero), or the line of action of the force intersects the axis (then the shoulder of the projection h=0). This fully corresponds to the physical meaning of the moment of force about the axis as a quantitative characteristic of the rotational effect of the force on a body having an axis of rotation.

g) body weight

It has long been noticed that under the action of force, a body gains speed gradually and continues to move if the force is removed. This property of bodies, to resist a change in their movement, was called inertia or inertia of bodies. The quantitative measure of the inertness of a body is its mass. Besides, body mass is a quantitative measure of the effect of gravitational forces on a given body the greater the mass of the body, the greater the gravitational force acting on the body. As shown below, NS These two definitions of body weight are related.

The rest of the concepts and definitions of dynamics will be discussed later in the sections where they first appear.

2. Bonds and bond reactions

Earlier in section 1, point (c), the concept of a free body was given, as a body that can move in space in any direction without being in direct contact with other bodies. Most of the real bodies that surround us are in direct contact with other bodies and cannot move in one direction or another. So, for example, bodies on the table surface can move in any direction, except for the direction perpendicular to the table surface downward. Doors fixed on hinges can rotate, but cannot move translationally, etc. Bodies that cannot move in space in one direction or another are called not free.

Anything that limits the movement of a given body in space is called constraints. It can be any other bodies that prevent the movement of this body in some directions ( physical connections); in a broader sense, it can be some conditions imposed on the movement of the body, limiting this movement. So, you can put a condition that the movement of a material point occurs along a given curve. In this case, the connection is specified mathematically in the form of an equation ( constraint equation). The question of the types of links will be discussed in more detail below.

Most of the connections imposed on bodies are practically physical connections. Therefore, the question arises about the interaction of this body and the connection imposed on this body. This question is answered by the axiom about the interaction of bodies: Two bodies act on each other with forces equal in magnitude, opposite in direction and located on the same straight line. These forces are called interaction forces. Interaction forces are applied to different interacting bodies. So, for example, when a given body and a connection interact, one of the interaction forces is applied from the side of the body to the connection, and the other interaction force is applied from the side of the connection to this body. This last power is called by the strength of the bond reaction or simply, communication reaction.

When solving practical problems of dynamics, it is necessary to be able to find the direction of reactions of various types of connections. The general rule of determining the direction of the bond reaction can sometimes help in this: The bond reaction is always directed opposite to the direction in which this bond prevents the movement of the given body. If this direction can be indicated definitely, then the reaction of the connection will be determined by the direction. Otherwise, the direction of the bond reaction is uncertain and can be found only from the corresponding equations of motion or equilibrium of the body. In more detail, the question of the types of connections and the direction of their reactions should be studied in the textbook: S.M. Targ A short course in theoretical mechanics "High school", M., 1986. Chapter 1, §3.

In section 1, point (c), it was said that the effect of any system of forces can be fully determined only if this system of forces is applied to a free body. Since most bodies, in reality, are not free, then in order to study the movement of these bodies, the question arises of how to make these bodies free. This question is answered axiom of lecture connections on philosophy at home. Lectures were... social psychology and ethnopsychology. 3. Theoretical Outcomes In social Darwinism there were ...

Theoretical Mechanics

Study Guide >> Physics

Abstract lectures on subject THEORETICAL MECHANICS For students of the specialty: 260501.65 ... - full-time Abstract lectures compiled on the basis of: L.V. Butorin, E.B. Busygin. Theoretical Mechanics... Training manual ...