Geometric location points. Theorem on the geometric location of points that are equidistant from two data points, in geometric and analytical forms
The geometric location on the plane is called the figure, which consists of all points of the plane with a specific property.
T.1.29. The geometric area of \u200b\u200bpoints equidistant from the two data points is a middle perpendicular to the segment connecting these points.
In Figure 71, a matted perpendicular of the SS was carried out to the cut. T.1.29 argues that: a) each point of direct equivalent from A and B; b) each point of the plane, equidistant from A and B, lies on a straight line
The following lists several geometric places of points on the plane.
1. The geometric location of the points at a given distance from this point is a circle with the center at this point and the radius equal to the distance.
2. The geometric location of the points at a given distance from a given direct consists of two straight lines, each of which is parallel to this and comes from it to this distance.
3. The geometrical location of points equidistant from two intersecting straight lines consists of two directs on which the bisector of all angles obtained when crossing direct data.
4. The geometric location of points, of which the segment is visible under this angle A and which lie on one side from the line A B, there is an arc of circumference with the ends at the points A and B.
The method of geometric seats used in solving tasks to build is based on the following.
Let us need to build a point X that satisfies two conditions. The geometric location of the points satisfying the first condition is a figure of a geometric area of \u200b\u200bpoints that satisfy the second condition, there is a figure the desired point X belongs, i.e. is their common point.
Example 1. Build around the perimeter, angle b, equal, and height, lowered from the vertex A.
Decision. Suppose the problem is solved and built (Fig. 72). Having postponing on a straight segment we will get an equifiable triangles
Based on the above reasoning, the construction can be carried out in the following sequence:


1) We carry out the straight and lay the segment on it
2) at a distance from straight spending straight parallel
3) with a vertex at point d Build an angle equal point
A is one of the vertices of the desired triangle.
4) We carry out the middle perpendicular to the segments of the point in and with the intersection of these middle perpendicular with the line - the other two vertices of the desired triangle.
Proof of the fact that the desired, we carry out: the height of this triangle is equal to the construction, isceived, - the external angle of this triangle, see T. 1. 22), by construction.
Possess some property.
Examples [ | ]
Formal definition[ | ]
In general, the geometric location of the points is formulated by a predicate, the argument of which is the point of this linear space. Predicate parameters can wear different types. Predicate is called determinant geometric point of points. Predicate parameters are called differentials The geometric location of the points (not to be confused with the differential in the analysis).
The role of differentials in the introduction of species differences in the figure. The number of differentials can be any; Differentials may not be at all.
If determined, where M (\\ DisplayStyle M) - point, differentials, then the desired figure A (\\ DisplayStyle A) Specify in the form of: " A (\\ DisplayStyle A) - geometric location points M (\\ DisplayStyle M)such that P (m, a, b, c, ...) (\\ displaystyle p (m, \\; a, \\; b, \\; c, \\; \\ ldots))" Further, it is usually indicated by the role of differentials, they are given names in relation to this particular figure. Under the actual figure understand the totality (set) points M (\\ DisplayStyle M)for which for each specific set of values a, b, c, ... (\\ displaystyle a, \\; b, \\; c, \\; \\ ldots) Statement P (m, a, b, c, ...) (\\ displaystyle p (m, \\; a, \\; b, \\; c, \\; \\ ldots)) Addresses to identity. Each specific set of differential values \u200b\u200bdetermines a separate figure, each of which and all of them in the aggregate are called the name of the figure, which is set via the GMT.
In the verbal wording, predicative statement is voiced by literary, that is, with the involvement of various kinds of revolutions, etc. With the aim of prowance. Sometimes, in the case of simple determinants, they generally cost without alleged designations.
Example: Parabola will ask as many all such points M (\\ DisplayStyle M)that the distance from M (\\ DisplayStyle M) to the point F (\\ DisplayStyle F) Equal distance from M (\\ DisplayStyle M) to direct L (\\ DisplayStyle L). Then Differentials Parabolas - F (\\ DisplayStyle F) and L (\\ DisplayStyle L); Determinant - Predicate P (m, f, l) \u003d (ρ (m, f) \u003d ρ l (m, l)) (\\ displaystyle p (m, \\; f, \\; l) \u003d (\\ rho (m, \\; f ) \u003d \\ rho _ (L) (m, \\; l)))where ρ (\\ DisplayStyle \\ Rho) - Distance between two points (metric), ρ L (\\ displaystyle \\ rho _ (L)) - distance from point to direct. And they say: "Parabola is a geometric location M (\\ DisplayStyle M)equivalent F (\\ DisplayStyle F) and direct L (\\ DisplayStyle L). Point F (\\ DisplayStyle F) refer to the focus of parabola, and the straight L (\\ DisplayStyle L) - Directress. "
Objectives lesson:
- Educational: show a new method for solving problems for building a geometric point of points; Teach to apply it in solving problems.
- Developing: development of visual-shaped thinking; Cognitive interest.
- Rising: Development of the ability to plan work, look for rational ways to fulfill its implementation, the ability to argued to defend their opinion, critically evaluate the result.
Tasks lesson:
- Studying a new material.
- Check the skill of students to solve problems.
Lesson plan:
- Definitions.
- Example 1.
- Example 2.
- Example 3.
- Theoretical part.
- Common matter.
Introduction
Ancient Egyptian and Babylonian culture in the field of mathematics continued the Greeks. They not only learned the entire experience of their geometry, but also went much further. Scientists ancient Greece They managed to bring accumulated geometric knowledge to the system and, thus, lay the start of geometry as deductive science.
Greek merchants got acquainted with East mathematics, laying trade routes. But the people of the East almost did not engage in theory, and the Greeks quickly discovered. They were asked: why in an equilibried triangle two angle at the base are equal; Why is the triangle area equal to half the area of \u200b\u200bthe rectangle with the same bases and heights?
Unfortunately, the first sources describing early period Development of Greek mathematics. Only due to the restored texts of the fourth century BC and the works of the Arab scientists, which were rich in translations of the writings of the authors of antique Greece, we have Euclidea publications, Archimedes, Apollonia and others great people. But in these works already represented quite developed mathematical science.
The mathematics of ancient Greece passed a long and difficult path of development, starting with the VI century BC. And by the 6th century. The historians of science are distinguished by three periods of its development in accordance with the nature of the knowledge:
- Accumulation of individual mathematical facts and problems (6 - 5b.b. BC).
- Systematization of the knowledge gained (4 - 3 V.V. BC).
- The period of computational mathematics (3B. BC - 6 V.).
Geometric points (GMT).
Definitions.
Geometric place - The term applied in the old literature on geometry and still used in the educational literature, to indicate sets of points satisfying a certain conditionis usually a geometric nature. For example: the geometric location of points equal to two points of points A and B is a mid-perpendicular to the AB segment. Sometimes they say about the geometric location of direct and other figures.
The name is associated with the presentation of the line as a "place" on which the points are located.
In the geometry trajectory of some point moving in accordance with this formula or condition. For example, a circle is a geometric point of the point moving on the plane so that the distance from the place of its location to the center remains unchanged.
Geometric location points (GMT) - This is a set of points in which all points fall, satisfy the definite condition, and only they.
Geometric location points (GMT) - Figure of speech in mathematics used to determine geometric Figure As many points with some property.
Examples.
- A middle perpendicular to the segment is a geometric area of \u200b\u200bpoints that are equidistant from the ends of the segment.
- The circle is a geometric area of \u200b\u200bpoints that are equidistant from this point, called the center of the circle.
- Parabola is a geometric area of \u200b\u200bpoints equid to the point (called focus) and a straight line (called director).
Example 1.
The middle perpendicular of any segment is a geometric point of points (that is, the set of all points) equal to the ends of this segment. Let P be perpendicular to AB and AO \u003d OB:
Then, the distances from any point p lying on the median perpendicular of Po, up to the ends of the A and B section of the AB are the same and equal to d.
Thus, each point of the median perpendicular segment has the following property: it is equal to the ends of the segment.
Example 2.
The bisector of the angle is a geometric area of \u200b\u200bpoints that are equidistant from his sides.
Example 3.
The circle is a geometric location of the points (that is, the set of all points) equal to its center (in fig. It is shown one of these points - a).
Chord, passing through the center of the circle (for example, Bc, Fig. 1) is called diameter and denotes d or d. Diameter- This is the greatest chord equal to two radius (D \u003d 2 R).
Tangent. Suppose the secant PQ (Fig. 2) passes through the points k and m of the circle. Suppose also that point M moves along the circle, approaching the point K. Then the secant PQ will change its position, rotating around the point K. As the point M is approached to the point K, the securing PQ will strive for a certain limit position of AV. Direct AB is called tangent to the circumference at the point K. Point K is called a touch point. Tanner and circle have only one common point - the touch point.
Properties tangent.
- Tanner to the circumference is perpendicular to the radius spent on the touch point (AB perpendicularly OK, Fig.2).
- From the point lying outside the circle, you can spend two tangents to the same circumference; Their segments are equal to AU \u003d AC (Fig. 3).
Segment- This is part of a circle bounded by an ACB arc and the corresponding chord of AB (Fig. 4). The length of the perpendicular CD spent from the middle of the chord AB to the intersection with the ACB arc is called the height of the segment.
Corners in a circle.
The central angle is an angle formed by two radius (∠aob, Fig. 5). Included angle - an angle formed by two chords of AB and AC conducted from their one common point (∠Bac, Fig.4). The angle described is an angle formed by two tangents of AB and AC, carried out from one common point (∠BAC, Fig.3).
Relations between the elements of the circle.
Inserted corner (∠ABC, Fig. 7) is equal to half of the central angle based on the same AMC arc (∠aoc, Fig.7). Therefore, all inscribed angles (Fig. 7), resting on the same arc (AMC, Fig. 7) are equal. And since the central angle contains the same number of degrees as its arc (AMC, Fig. 7), then any of the inscribed angle is measured half an arc to which it relies (in our case AMC).
All inscribed angles based on semicircle (∠apb, ∠aqb, ..., Fig. 8), straight.
Angle(∠aod, Fig. 9), formed by two chords (AB and CD), is measured by half an arcs concluded between its parties: (and + CMB) / 2.
The angle (∠aod, Fig. 10), formed by two secuchs (AO and OD), is measured by the height of the arcs concluded between its parties: (and - BMC) / 2.
The angle (∠dcb, fig.11), formed by tangent and chord (AB and CD), is measured by half an arc enclosed inside it: CMD / 2.
The angle (∠Boc, Fig.12), formed by the tangent and secant (CO and BO), is measured by the height of the arcs concluded between its parties: (BMC - CND) / 2.
The described angle (∠AOC, Fig. 12), formed by two tangents (CO and AO), is measured by the height of the arcs concluded between its parties: (ABC - CDA) / 2.
The works of chord segments (AB and CD, Fig.13 or Fig.14), for which they are divided by the intersection point, are equal to: AO · BO \u003d CO · DO.
The tangential square is equal to the product of the section on its external part (Fig. 12): OA 2 \u003d OB · OD. This property can be considered as a special case Fig.14.
Chord(AB , Fig.15) perpendicular diameter(CD) , O.in half: AO \u003d OB.
Fig. fifteen
Interesting fact:
Congratulations on the pi-teller you.

I expressed scientific language, the number "PI" is the ratio of the circumference length to its diameter. Simple seems to be a thing, but concerns the minds of mathematicians with deep antiquity. And continues to worry. To such an extent that scientists - 20 years ago - agreed to celebrate the holiday of this number. And they encouraged to join the celebrations of the entire progressive public. She joins: Eats round Pi-Rogs, you are-pi-watts, be sure to pi and publishes the sounds of Pi at a meeting.
Fans will compete, remembering the signs of the number "PI". And they will try to surpass a record of a 24-year-old Chinese student Liu Chao, who called the memory without errors of 68890 characters. It went on it 24 hours and 4 minutes.
The shipment of celebrations is scheduled for March 14 - a date, which in American writing looks like 3.14 - that is, the first three numbers of the number "PI".
According to the legend, the Babylonian priests knew about the number of "pi". Used in construction Babylonian tower. But they could not accurately calculate its meaning and did not cope with this project. The symbol of the number "Pi" first used in his writings in 1706 by William Jones (William Jones). But really he passed on after 1737 due to the efforts of the Swedish Mathematics Leonard Euler (Leonhard Euler).
Mounting a holiday came up with American physicist Larry Sew (Larry Shaw).
To the question of how many signs among the number "Pi" after the comma, there is no accurate answer. Most likely, their infinite number. BUT main feature The fact that the sequence of these characters is not repeated. Today they are known 12411 trillion. Surveyed 500 billion. And the repetitions were not found.
According to some prominent physics and mathematics, such as David Bailey, Peter Borvin and Simon Borevel (David Bailey, Peter Borewin, Simon Plouffe), their repetitions - not to find anyone and never. Although I spoke the all the universe signs. Yes, at least how many universes ... and in this scientists see some hidden mysticism. It is believed that in the number of "PI" an endless primary chaos is encrypted, which later became harmony. Or some kind of mysterious information.

Questions:
- Word the circumformation of the circle and the circle?
- What new concepts did you meet?
- What is called a geometric point of points?
- What is the difference between diameter and radius?
- How to find a circle radius which is described near the triangle?
List of sources used:
- Lesson on the topic "Visual Geometry"
- Savin A.P. Method of geometric places / Optional course in mathematics: Tutorial For 7-9 classes high School. Cost. I.L. Nikolskaya. - M.: Enlightenment, p. 74.
- Smirnova I.M., Smirnov V.A. Geometry: Tutorial for 7-9 classes general educational institutions. - M.: Mnemozina, 2005, p. 84.
- Sharygin I.F. Geometry. 7-9 Classes: Textbook for general education educational institutions. - M.: Drop, p. 76.
- Mazur K. I. "Solution of the main competitive tasks in mathematics of the collection edited by M. I. Scanavi"
Over the lesson worked:
Samina M.V.
Purknak S.A.
Vladimir Lagovsky
Put a question about O. modern education, express the idea or solve the urebral problem you can Educational forum Where at the international level the educational council of fresh thoughts and action is going. Creation blog You will not only increase your status as a competent teacher, but also make a significant contribution to the development of the school of the future. Guild of Leaders of Education Opens the doors for top rank specialists and invites to cooperate in the direction of creating the world's best schools.
Geometric location points. Municipal perpendicular. Bisektris corner.
Circle. A circle . Center of the circle. Radius. Arc. Secant. Chord.
Diameter. Tangent and its properties. Segment. Sector. Corners in a circle.
Dougie Length . Radian. Relations between the elements of the circle.
Geometric locostochki – eNGLISH all Points, satisfying the defined specified Conditions.
PRI M E P 1. Median perpendicular of any segment is geometric
place of points (i.e., many points), Equalued oT
the ends of this segment. Let Po AB and AO \u003d OB:
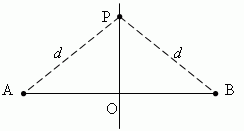
Then distances from any pointP. lying on the median perpendicularPo, up to the ends of A and B Cut AB same and equald.
In this way, each point of the middle perpendicular Cut It has the following property: it is equal to the ends of the segment.
PRI ME P 2. Bisector corner there is Geometric location of points equidalized from his sides .
PRI ME R 3 . The circle is a geometric point of points (i.e. gUSTs
all points), Equalued from her center (in fig. until uAV alone
from these points - a).

Circle - this is geometric location points (i.e. set all points) on the plane , Equalued From one point,called the center of the circle. The segment connecting the center of the circle with some kind of its point is called radius And denotesr. or R.. Part of the plane limited by a circle called around. Part of the circle (
A. m.B, Fig.39) called arc. Straight PQ, Passing through Points M. and N. Circle (Fig.39 ), called splitand its cut MN. lying inside - chord.
Chord passing through the center of the circle (for example,
BC. , Fig.39), calleddiameter And denotes d. or D.Diameter is the greatest chord equal to two radiities (d.= 2 r.).
Tangent. Suppose, sequentialPQ. (Fig. 40) passes through pointsK and M. Circle. Suppose also that pointM. moving along the circle, approaching the pointK. Then the secant PQ will change your position, rotating around the pointK. . As the point approachesM to point K Sequer PQ Will strive for some limit position of AV. StraightAB called tangent to circle at pointK. Point K. called touchpoint. Tanner and circle have only one common point - the touch point.
Properties tangent.
1) TOasient to the circle perpendicular to the radius carried out to the point of touch(AB OK, Fig.40) .
2) From the point lying outside the circle, you can spend two tangents to
same circumference; their segments are equal (Fig.41).
Segment - This is part of the circle, limited arcACB. and the corresponding chordaAB (Fig.42). Length perpendicularCD conducted from the middle of the chord AB before intersection with arcACB. , called height segment.
Sector – etceath the circle limited to the arcA. m.B. and two radiusOAI OB, conducted to the ends of this arc (Fig.43).
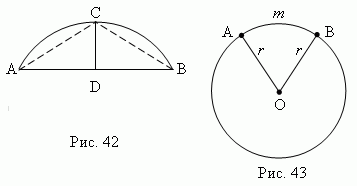
Corners in a circle. Central corner – angle formed by two radii ( AOB fig.43). Inserted corner - angle formed by two chordsAB and AC conducted from their one common point (BA C, Fig.44). Described corner - angle formed by two tangentsAB and AC conducted from one common point ( BAC, Fig.41).

Dougie Length the circle is proportional to its radius R. and the corresponding central corner :
l \u003d. r.
So, if we know the length of the arc
l. and radius r., then the magnitude of the corresponding central angle it can be determined by their attitude: \u003d L / R.This formula is the basis for determining radian dimension Corners. So, if L. = r,that \u003d 1, and we say the angle equal to 1 radiane (this is indicated: = 1 glad). So we have next definition Radian as units of measurement of angles: radian is a central angle ( AOB, Fig.43), in which the length of the arc is equal to its radius (A. m.B \u003d AO, Fig.43). So, the radiant measure of any angle is the ratio of the length of the arc, conducted by an arbitrary radius and the prisoner between the sides of this angle, to its radius.In particular, in accordance with the formula of the length of the arc, the length of the circleC. It can be expressed as follows:
where Determined as attitudesC. To the diameter of the circle 2r. :
= C /2 r.
Irrational number; Its approximate value 3.1415926…
On the other hand, 2- this is circular corner The circle, which in the degree measurement system is 360º. In practice, it often happens that both the radius of the arc and the angle are unknown. In this case, the length of the arc can be calculated by the approximate Guigens formula:
p. 2l. + (2l - L.) / 3 ,
where (see Fig.42): p. - Arc length ACB; l. - Length of chords AC; L. - Length chords AB. If the arc contains no more than 60º , the relative error of this formula does not exceed 0.5%.
Relations between the elements of the circle. Inserted corner ( ABC, Fig.45) equal to half of the central angle , resting on the same arc A. mC. ( AOC., Fig.45) . Therefore, all inscribed angles(Fig.45), relying on one and T. the same arc (A. m.C. , Fig.45), equal.And since the central angle contains also the number of degrees that his arc ( A. m.C. , Fig.45), then any inscribed angle is measured half an arc to which it rests(in our case A. m.C).

All inscribed angles relying on semicircle (APB, AQB, ..., Fig.46), straight (Prove it, please!).
Angle(AOD, Fig.47 )chord(ABI CD) measures semi-mounted arcs concluded between his parties: (A. n.D + C. m.B) / 2.

Angle(AOD, Fig.48) , formed by two secantia (AOO OD. ), it is measured by the height of the arcs, prisoners between his parties: (A. n.D- B. m.C. ) / 2. sale(COI BO. ), measured by semi-definition Arcs concluded between his parties: (B. m.C. – C. n.D. ) / 2 .

Described corner(AOC, Fig.50 )two-tanged(COI AO. ), it is measured by the height of the arcs concluded between its Parties: (ABC. – CDA) / 2 .
Works of segments of chord (AB and CD , Fig.51 or Fig. 52), which they share the intersection point, equal: AO · BO \u003d CO · DO.
The tangential is equal to the product of the sequential on its external part (Fig. 50): OA 2 \u003d OB · o D (Prove!). This property can be viewed as a special case. Fig.52.

Chord(AB , Fig.53) perpendicular diameter(CD )is divided at their intersection point O. in half:AO \u003d OB.
( Try to prove it!).
Possess some property.
Encyclopedic YouTube.
1 / 3
✪ Definition of parabola as a GMT
✪ 124. Tasks on the second order surface. Geometric location
✪ resistance of materials. Lecture 21 (stress tensor, main stresses)
Subtitles
Hello, dear friends! We will now be geometry with you now, and then algebra, and then we all mix and let's call it mathematics. Very simple question. Imagine that where I put a white point playing music (one column). And then the technician appeared and put the column also at the place of the pink point. And the distance between them is quite large. If you put in a green cross, then for you the music will be coming from two places with a delay. From one with a greater delay than from the other. How to get up so that you hear the music with the left and right ear is exactly the same, synchronously? That is, stand at equal distances from two columns. The answer is very simple, you, of course, know if at least grade 7 went. And if you did not go, you can guess intuitively. It is necessary to build a segment connecting pink and white dots, and in its center (in its middle), depict perpendicular. Then any point of vertical on this board perpendicular is equally removed from the pink and white. Why is that? Very simple. Here are two identical triangles. Why are they the same? Because they have a common party, two more parties are marked with equal strokes. And straight corners are also, of course, are equal to each other. As a result, we have the right to put equal marks on such parties. So, we painted the geometric location of the points equally deleted from the two set points. What about two direct? Let's draw a couple of straight lines. I paint two parallel straight lines to begin. These are two shores and you want to swim (for some reason) on equal deletes from these two shores. How to build this trajectory? Let's build a perpendicular again to two parallel straight. We will find his heart. And then, armed with the eye meter, trying to portray the green line in parallel with these two shores. Of course, if we take any point on this green line and lower the perpendicular to some shore, then we can see the rectangle. So, these parties will be equal. Straight can and intersect. And then you also easily solve such a task: a variety of points, equally distant from these two straight lines is a pair of bisector. All these solutions are built with a circulation and a ruler and completely easily passing on geometry. And now I will offer you another set, which is not given not two of the same objects, and we take one object from the first task: somewhere it is worth the point, and the other object is from the second: there is a straight line. And this point we need for a long time, so we will introduce her personal name: we will say that it is point F. The straight line is also personalized and called the letter d. Imagine for a moment that this is the beach border: above the beach, and below the sea. And the point F is, for example, a kiosk with ice cream. And you want to sit so that to the kiosk with ice cream and to the shore there was an equal distance. Then an example of such a place is absolutely obvious: just like here, and here, we build a perpendicular from point F to direct d, find it a heart and this is the most winning place: you have very little to go to the kiosk and go to the sea very little . And how can I sit in a different way, so that it was also the same distance to the kiosk, and before the shores of the sea? Here is an example one more. If we build a square with such a party, then the equality of these sides and perpendicular here also guarantee us that this point is suitable. Moreover, it is clear that once the yarn stretches in both directions, then here we can draw the same square. The solution will be symmetrically. Let's write a solution for such a task. We are looking for this: we need a lot of letters M (points designated by the letter M), and the condition for them is what: (this one is suitable to be the letter M) the distance from any point from this set to F is equal ... instead of the word "Distance "I'll write the letter" RO ", because I want the distance from point m to a straight line d. Since we are looking for a lot, there are curly braces. And we are looking for all such points indicated by the letter M to be carried out by this equality. Two we have already found. I have the right to circle this point with a green circle and this too. Is there any other point between them that belongs to this set? Equally removed from F, and from D. Yes there is. Let's try to do the following. Sharing on some value to the left of the points known to us from the set. Question: Then we get a point from the same set? Let's look at this figure, on this quadrilateral. This is a rectangle, so here you also say one touch. The distance from the resulting point to F as connected with this segment? Of course, it is more, here it is impossible to put one touch, because such a sloping segment is hypothinuse in a triangle, where catat is marked with one touch. This point is too low, too close to a straight line d. So, it is necessary to lift it a little. Raise so much so that it is quite removed from D and slightly approached F. How exactly will not find out, but it is possible. The idea is this: moving to the left and climbing up, we can get the points belonging to the set M. and if you still assume that the step may be small, then we will understand that the lot is continuous: this is a line that you can draw a hand moving without stopping And nowhere is not jumping. And we also know that the line is symmetrical. This green line is an image of this set, designated by figure brackets. It turns out that Parabola. This is a geometric definition for a parabola. And there are problems.
Examples
The role of differentials in the introduction of species differences in the figure. The number of differentials can be any; Differentials may not be at all.
If determined, where M (\\ DisplayStyle M) - point, differentials, then the desired figure A (\\ DisplayStyle A) Specify in the form of: " A (\\ DisplayStyle A) - geometric location points M (\\ DisplayStyle M)such that P (m, a, b, c, ...) (\\ displaystyle p (m, \\; a, \\; b, \\; c, \\; \\ ldots))" Further, it is usually indicated by the role of differentials, they are given names in relation to this particular figure. Under the actual figure understand the totality (set) points M (\\ DisplayStyle M)for which for each specific set of values a, b, c, ... (\\ displaystyle a, \\; b, \\; c, \\; \\ ldots) Statement P (m, a, b, c, ...) (\\ displaystyle p (m, \\; a, \\; b, \\; c, \\; \\ ldots)) Addresses to identity. Each specific set of differential values \u200b\u200bdetermines a separate figure, each of which and all of them in the aggregate are called the name of the figure, which is set via the GMT.
In the verbal wording, predicative statement is voiced by literary, that is, with the involvement of various kinds of revolutions, etc. With the aim of prowance. Sometimes, in the case of simple determinants, they generally cost without alleged designations.
Example: Parabola will ask as many all such points M (\\ DisplayStyle M)that the distance from M (\\ DisplayStyle M) to the point F (\\ DisplayStyle F) Equal distance from M (\\ DisplayStyle M) to direct L (\\ DisplayStyle L). Then Differentials Parabolas - F (\\ DisplayStyle F) and L (\\ DisplayStyle L); Determinant - Predicate P (m, f, l) \u003d (ρ (m, f) \u003d ρ l (m, l)) (\\ displaystyle p (m, \\; f, \\; l) \u003d (\\ rho (m, \\; f ) \u003d \\ rho _ (L) (m, \\; l)))where ρ (\\ DisplayStyle \\ Rho) - Distance between two points (metric), ρ L (\\ displaystyle \\ rho _ (L)) - distance from point to direct. And they say: "Parabola is a geometric location M (\\ DisplayStyle M)equivalent F (\\ DisplayStyle F) and direct L (\\ DisplayStyle L). Point F (\\ DisplayStyle F) refer to the focus of parabola, and the straight L (\\ DisplayStyle L) - Directress. "