Геометричне місце точок. Теорема про геометричному місці точок, рівновіддалених від двох даних точок, в геометричній і аналітичної формах

Геометричним місцем точок на площині називається фігура, яка складається з усіх точок площини, що володіють певним властивістю.

Т.1.29. Геометричне місце точок, рівновіддалених від двох даних точок, є серединний перпендикуляр до відрізка, що з'єднує ці точки.

На малюнку 71 до відрізка проведено серединний перпендикуляр СС. Т.1.29 стверджує, що: а) кожна точка прямої рівновіддалена від А і В; б) кожна точка площини, рівновіддалена від А і Б, лежить на прямій

Нижче перераховані кілька геометричних місць точок на площині.

1. Геометричне місце точок, що знаходяться на даному відстані від даної точки, є коло з центром в цій точці і радіусом, рівним даному відстані.

2. Геометричне місце точок, що знаходяться на даному відстані від даної прямої, складається з двох прямих, кожна з яких паралельна даній і відстоїть від неї на дане відстань.

3. Геометричне місце точок, рівновіддалених від двох пересічних прямих, складається з двох прямих, на яких лежать бісектриси всіх кутів, отриманих при перетині даних прямих.

4. Геометричне місце точок, з яких відрізок видно під даним кутом а і які лежать по одну сторону від прямої А Б, є дуга окружності з кінцями в точках А і Б.

Метод геометричних місць, застосовуваний при вирішенні задач на побудову, заснований на наступному.

Нехай нам треба побудувати точку X, що задовольняє двом умовам. Геометричне місце точок, що задовольняють першому умові, є фігура геометричне місце точок, що задовольняють другій умові, є фігура Шукана точка X належить, т. Е. Є їхньою спільною точкою.

Приклад 1. Побудувати по периметру, розі Б, рівного, і висоті, опущеною з вершини А.

Рішення. Нехай задача вирішена і побудований (рис. 72). Відклавши на прямий відтинки отримаємо трикутник

Виходячи з наведених вище міркувань побудова можна здійснити в наступній послідовності:

1) Проводимо пряму і на ній відкладаємо відрізок

2) На відстані від прямої проводимо пряму паралельну

3) З вершиною в точці D будуємо кут рівний Точка

А - одна з вершин шуканого трикутника.

4) Проводимо серединні перпендикуляри до відрізків Точки В і С перетину цих серединних перпендикулярів з прямою - дві інші вершини шуканого трикутника.

Доказ того, що шуканий, проводимо так: висота цього трикутника дорівнює з побудови, рівнобедрений, - зовнішній кут цього трикутника, см. Т. 1. 22), з побудови.

Що володіють деяким властивістю.

приклади [ | ]

формальне визначення[ | ]

У загальному випадку, геометричне місце точок формулюється предикатом, аргументом якого є точка даного лінійного простору. Параметри предиката можуть носити різний тип. предикат називається детермінантою геометричного місця точок. Параметри предиката називаються диференціалами геометричного місця точок (не плутати з диференціалом в аналізі).

Роль диференціалів у введенні видових відмінностей в фігуру. Кількість диференціалів може бути будь-яким; диференціалів може і зовсім не бути.

Якщо задані детермінант, де M (\\ displaystyle M) - точка, - диференціали, то шукану фігуру A (\\ displaystyle A) задають у вигляді: « A (\\ displaystyle A) - геометричне місце точок M (\\ displaystyle M), Таких, що P (M, a, b, c, ...) (\\ displaystyle P (M, \\; a, \\; b, \\; c, \\; \\ ldots))». Далі зазвичай вказується роль диференціалів, їм даються назви стосовно даної конкретної фігури. Під власне фігурою розуміють сукупність (безліч) точок M (\\ displaystyle M), Для яких для кожного конкретного набору значень a, b, c, ... (\\ displaystyle a, \\; b, \\; c, \\; \\ ldots) вислів P (M, a, b, c, ...) (\\ displaystyle P (M, \\; a, \\; b, \\; c, \\; \\ ldots)) звертається в тотожність. Кожен конкретний набір значень диференціалів визначає окрему фігуру, кожну з яких і всіх їх в сукупності називають назвою фігури, яка задається через ГМТ.

У словесній формулюванні предикативное висловлювання озвучують літературно, тобто із залученням різного роду оборотів і т. Д. З метою милозвучності. Іноді, в разі простих детермінантів, взагалі обходяться без літерних позначень.

приклад: Параболу задамо як безліч всіх таких точок M (\\ displaystyle M), Що відстань від M (\\ displaystyle M) до точки F (\\ displaystyle F) дорівнює відстані від M (\\ displaystyle M) до прямої l (\\ displaystyle l). Тоді диференціали параболи - F (\\ displaystyle F) і l (\\ displaystyle l); детермінант - предикат P (M, F, l) \u003d (ρ (M, F) \u003d ρ l (M, l)) (\\ displaystyle P (M, \\; F, \\; l) \u003d (\\ rho (M, \\; F ) \u003d \\ rho _ (l) (M, \\; l))), де ρ (\\ displaystyle \\ rho) - відстань між двома точками (метрика), ρ l (\\ displaystyle \\ rho _ (l)) - відстань від точки до прямої. І кажуть: «Парабола - геометричне місце точок M (\\ displaystyle M), Рівновіддалених від точки F (\\ displaystyle F) і прямий l (\\ displaystyle l). крапку F (\\ displaystyle F) називають фокусом параболи, а пряму l (\\ displaystyle l) - директоркою ».

Мета уроку:

Освітня: показати новий метод вирішення завдань на побудова геометричного місця точок; Навчити застосовувати його в рішенні задач.
Розвиваюча: розвиток наочно-образного мислення; пізнавального інтересу.
Виховує: розвиток вміння планувати роботу, шукати раціональні шляхи її виконання, здатності аргументовано відстоювати свою думку, критично оцінювати результат.

Завдання уроку:

Вивчення нового матеріалу.
Перевірити вміння учнів розв'язувати задачі.

План уроку:

Визначення.
Приклад 1.
Приклад 2.
Приклад 3.
Теоретична частина.
Спільні поняття.

Вступ.

Давньоєгипетську і вавилонську культуру в області математики продовжували греки. Вони не тільки засвоїли весь досвід їх геометрії, а й пішли набагато далі. вчені стародавньої Греції зуміли привести в систему накопичені геометричні знання і, таким чином, залежить початку геометрії як дедуктивної науки.

Грецькі купці познайомилися зі східною математикою, прокладаючи торгові шляхи. Але люди Сходу майже не займалися теорією, і греки швидко це виявили. Вони ставили собі питання: чому в трикутник два кута при основі рівні; чому площа трикутника дорівнює половині площі прямокутника при однакових підставах і висотах?

На жаль, не збереглося першоджерел, що описують ранній період розвитку грецької математики. Тільки завдяки відновленим текстам четвертого століття до нашої ери і працям арабських вчених, які були багаті перекладами творів авторів античної Греції, ми маємо в своєму розпорядженні виданнями Евкліда, Архімеда, Аполлонія і інших великий людей. Але в цих творах вже представлена \u200b\u200bцілком розвинена математична наука.

Математика стародавньої Греції пройшла тривалий і складний шлях розвитку, починаючи з VI століття до н.е. і по VI століття. Історики науки виділяють три періоди її розвитку відповідно до характеру знань:

накопичення окремих математичних фактів і проблем (6 - 5B.B. до н.е.).
Систематизація отриманих знань (4 - 3 ст до н.е.).
Період обчислювальної математики (3в. До н.е. - 6 ст.).

Геометричне місце точок (ГМТ).

Визначення.

геометричне місце - термін, що застосовувався в старій літературі з геометрії і до сих пір застосовується в навчальній літературі, для позначення безлічі точок, які відповідають деякому умові, Як правило, геометричного характеру. Наприклад: геометричне місце точок, рівновіддалених від двох даних точок A і B - це серединний перпендикуляр до відрізка AB. Іноді говорять і про геометричному місці прямих і інших фігур.

Назва пов'язана з поданням про лінії як про «місці», на якому розташовуються точки.

В геометрії траєкторія деякої точки, що переміщається відповідно до даної формулою або умовою. Наприклад, коло є геометричним місцем точки, що переміщається на площині так, що відстань від місця її знаходження до центру залишається незмінним.

Геометричне місце точок (ГМТ) - це безліч точок, в яке потрапляють всі точки, що задовольняють певній умові, і тільки вони.

Геометричне місце точок (ГМТ) - фігура мови в математиці, що вживається для визначення геометричної фігури як безлічі точок, які мають деяким властивістю.

Приклади.

Серединний перпендикуляр до відрізка є геометричне місце точок, рівновіддалених від кінців відрізка.
Окружність є геометричне місце точок, рівновіддалених від даної точки, званої центром кола.
Парабола є геометричне місце точок, рівновіддалених від точки (званої фокусом) і прямий (званої директоркою).

Приклад 1.

Серединний перпендикуляр будь-якого відрізка є геометричне місце точок (тобто безліч всіх точок), рівновіддалених від кінців цього відрізка. Нехай PO перпендикулярно AB і AO \u003d OB:

Тоді, відстані від будь-якої точки P, що лежить на серединному перпендикуляре PO, до кінців A і B відрізка AB однакові і рівні d.

Таким чином, кожна точка серединного перпендикуляра відрізка має наступну властивість: вона рівновіддалена від кінців відрізка.

Приклад 2.

Бісектриса кута є геометричне місце точок, рівновіддалених від його сторін.

Приклад 3.

Окружність є геометричне місце точок (тобто безліч всіх точок), рівновіддалених від її центру (на рис. Показана одна з цих точок - А).

хорда, Що проходить через центр кола (наприклад, BC, рис 1), називається діаметром і позначається d або D. Діаметр- це найбільша хорда, що дорівнює двом радіусів (d \u003d 2 r).

дотична. Припустимо, січна PQ (рис.2) проходить через точки K і M окружності. Припустимо також, що точка M рухається уздовж окружності, наближаючись до точки K. Тоді січна PQ буде міняти своє положення, обертаючись навколо точки K. У міру наближення точки M до точки K січна PQ буде прагнути до деякого граничного стану АВ. Пряма AB називається дотичною до кола в точці K. Точка K називається точкою дотику. Дотична і коло мають тільки одну спільну точку - точку дотику.

Властивості дотичної.

Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику (AB перпендикулярно OK, рис.2).
З точки, що лежить поза колом, можна провести дві дотичні до однієї і тієї ж кола; їх відрізки рівні АВ \u003d АС (рис.3).

сегмент- це частина круга, обмежена дугою ACB і відповідної хордою AB (рис.4). Довжина перпендикуляра CD, проведеного з середини хорди AB до перетину з дугою ACB, називається висотою сегмента.

Кути в колі.

Центральний кут - кут, утворений двома радіусами (∠AOB, рис.5). Вписаний кут - кут, утворений двома хордами AB і AC, проведеними з їх однією загальної точки (∠BAC, рис.4). Описаний кут - кут, утворений двома дотичними AB і AC, проведеними з однієї загальної точки (∠BAC, рис.3).

Співвідношення між елементами кола.

вписаний кут (∠ABC, рис.7) дорівнює половині центрального кута, що спирається на ту ж дугу AmC (∠AOC, рис.7). Тому, все вписані кути (рис.7), що спираються на одну й ту ж дугу (AmC, рис.7), рівні. А так як центральний кут містить таку саму кількість градусів, що і його дуга (AmC, рис.7), то будь-який вписаний кут вимірюється половиною дуги, на яку він спирається (в нашому випадку AmC).

Всі вписані кути, що спираються на півколо (∠APB, ∠AQB, ..., рис.8), прямі.

кут(∠AOD, рис.9), утворений двома хордами (AB і CD), вимірюється напівсумою дуг, укладених між його сторонами: (AnD + CmB) / 2.

Кут (∠AOD, рис.10), утворений двома січними (AO і OD), вимірюється Полуразность дуг, укладених між його сторонами: (AnD - BmC) / 2.

Кут (∠DCB, рис.11), утворений дотичною і хордою (AB і CD), вимірюється половиною дуги, укладеної всередині нього: CmD / 2.

Кут (∠BOC, рис.12), утворений дотичною і січною (CO і BO), вимірюється Полуразность дуг, укладених між його сторонами: (BmC - CnD) / 2.

Описаний кут (∠AOC, рис.12), утворений двома дотичними (CO і AO), вимірюється Полуразность дуг, укладених між його сторонами: (ABC - CDA) / 2.

Твори відрізків хорд (AB і CD, рис.13 або рис.14), на які вони поділяються точкою перетину, рівні: AO · BO \u003d CO · DO.

Квадрат дотичній дорівнює добутку січної на її зовнішню частину (рис.12): OA 2 \u003d OB · OD. Це властивість можна розглядати як окремий випадок рис.14.

хорда(AB , Рис.15) , Перпендикулярна діаметру(CD) , Oнавпіл: AO \u003d OB.

Мал. 15

Цікавий факт:

Вітаємо з Пі-раздніком вас.

Висловлюючись науковою мовою, число "Пі" - це відношення довжини окружності до її діаметра. Проста начебто річ, але хвилює розуми математиків з глибокої давнини. І продовжує хвилювати. До такої міри, що вчені - років 20 назад - домовилися відзначати свято цього числа. І закликали приєднатися до урочистостей всю прогресивну громадськість. Вона приєднується: їсть круглі Пі-роги, ви-ПІ-кість, обов'язково Пі-во і видає звуки Пі при зустрічі.

Фанати будуть змагатися, згадуючи знаки числа "Пі". І постараються перевершити рекорд 24-річного китайського студента Лю Чао, який назвав по пам'яті без помилок 68890 знаків. На це у нього пішло 24 години і 4 хвилини.

Відправлення урочистостей призначено на 14 березня - дату, яка в американському написанні виглядає як 3.14 - тобто, першими трьома цифрами числа "Пі".
За легендою, про число "Пі" знали ще вавилонські жерці. Використовували при будівництві Вавилонської вежі. Але не змогли точно обчислити його значення і від цього не впоралися з проектом. Сам символ числа "Пі" вперше використав у своїх працях в 1706 році математик Вільям Джон (William Jones). Але реально він прижився після 1737 року завдяки старанням шведського математика Леонарда Ейлера (Leonhard Euler).

Відзначати свято придумав американський фізик Ларрі Шо (Larry Shaw).
На питання, скільки знаків у числі «Пі» після коми, точної відповіді немає. Швидше за все, їх нескінченне число. А головна особливість в тому, що послідовність цих знаків не повторюється. Сьогодні їх відомо 12411 трильйонів. Обстежено 500 мільярдів. І повторень, не знайдено.

Як вважають деякі видні фізики і математики, наприклад Девід Бейлі, Пітер Борвін і Саймон Плофе (David Bailey, Peter Borewin, Simon Plouffe), їх - повторень - годі й шукати нікому і ніколи. Хоч іспіші знаками весь Всесвіт. Та хоч скільки Всесвітів ... І в цьому вчені бачать якусь приховану містику. Вважають, що в числі "Пі" зашифрований нескінченний первородний хаос, що став потім гармонією. Або якась загадкова інформація.

питання:

Сформулюйте визначення кола і кола?
З якими новими поняттями ви познайомилися?
Що називається геометричним місцем точок?
Яка різниця між діаметром і радіусом?
Як знайти радіус кола яка описана навколо трикутника?

Список використаних джерел:

Урок на тему "Наочна геометрія"
Савін А.П. Метод геометричних місць / Факультативний курс з математики: Навчальний посібник для 7-9 класів середньої школи. Упоряд. И.Л. Нікольська. - М .: Просвещение, с. 74.
Смирнова І.М., Смирнов В.А. Геометрія: Підручник для 7-9 класів загальноосвітніх установ. - М .: Мнемозина, 2005, с. 84.
Шаригін І.Ф. Геометрія. 7-9 класи: Підручник для загальноосвітніх учбових закладів. - М .: Дрофа, с. 76.
Мазур К. І. «Рішення основних конкурсних завдань з математики збірника під редакцією М. І. Сканаві»

Над уроком працювали:

Самилін М.В.

Потурнак С.А.

Володимир Лаговський

Поставити питання про сучасній освіті, Висловити ідею або вирішити назрілу проблему Ви можете на освітньому форумі , Де на міжнародному рівні збирається освітня рада свіжої думки і дії. створивши блог, Ви не тільки підвищите свій статус, як компетентного викладача, а і зробите вагомий внесок в розвиток школи майбутнього. Гільдія Лідерів Освіти відкриває двері для фахівців вищого рангу і запрошує до співпраці в напрямку створення кращих в світі шкіл.

Геометричне місце точок. серединний перпендикуляр. Бісектриса кута.

Окружність. коло . Центр кола. Радіус. Дуга. Січна. Хорда.

Діаметр. Дотична і її властивості. Сегмент. Сектор. Кути в колі.

довжина дуги . Радіан. Співвідношення між елементами кола.

геометричне местоточек – етомножество всіх точок, задовольня ющіхопределённим заданим умовами.

П р и м і р 1. Серединний перпендикуляр будь-якого відрізка є геометричне

місце точок (тобто безліч всіх точок), рівновіддалений них від

решт цього відрізка. Нехай PO AB і AO \u003d OB:

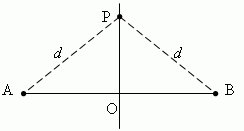
Тоді, відстані від будь-якої точкиP , Що лежить на серединному перпендикуляреPO, до кінців A і B відрізка AB однакові і рівніd.

Таким чином, кожна точка серединного перпендикуляра відрізка має наступну властивість: вона рівновіддалена від кінців відрізка.

П р и м і р 2. бісектриса кута є геометричне місце точок, рівновіддалених від його сторін .

П р и м і р 3 . Окружність є геометричне місце точок (тобто множе ство

всіх точок), рівновіддалених від її центру (на рис. Бувай зана одна

з цих точок - А).

окружність - це геометричне місце точок (тобто безліч всіх точок) на площині , рівновіддалених від однієї точки,званої центром кола. Відрізок, що з'єднує центр кола з будь-якої її точкою, називається радіусом і позначаєтьсяr або R. Частина площини, обмежена колом, називається кругом. частина окружності (

A mB, рис.39) називається дугою. пряма PQ, що проходить через точки M і N кола (рис.39 ), Називається січною,а її відрізок MN , Що лежить всередині кола - хордою.

Хорда, що проходить через центр кола (наприклад,BC , Рис.39), називаєтьсядіаметром і позначається d або D.Діаметр - це найбільша хорда, що дорівнює двом радіусів (d= 2 r).

Дотична. Припустимо, січнаPQ (Рис.40) проходить через точкиK і M окружності. Припустимо також, що точкаM рухається уздовж окружності, наближаючись до точкиK. Тоді січна PQ буде міняти своє положення, обертаючись навколо точкиK . У міру наближення точкиM до точки K січна PQ буде прагнути до деякого граничного стану АВ. прямаAB називається дотичній до кола в точціK. Точка K називається точкою дотику. Дотична і коло мають тільки одну спільну точку - точку дотику.

Властивості дотичної.

1) Доасательная до кола перпендикулярна до радіуса, проведеного в точку дотику(AB OK, рис.40) .

2) З точки, що лежить поза колом, можна провести дві дотичні до однієї і тієї ж кола; їх відрізки рівні (Рис.41).

сегмент - це частина кола, обмежена дугоюACB і відповідної хордоюAB (Ріс.42). довжина перпендикуляраCD , Проведеного з середини хорди AB до перетину з дугоюACB , називається висотою сегмента.

сектор – еточасть кола, обмежена дугоюA mB і двома радіусамиOAі OB, проведеними до кінців цієї дуги (рис.43).

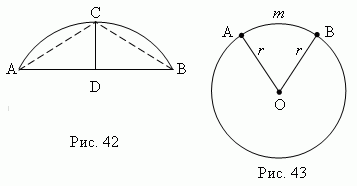
Кути в колі. центральний кут – кут, утворений двома радіусами ( AOB, рис.43). вписаний кут - кут, утворений двома хордамиAB і AC , Проведеними з їх однією загальною точки (BA C, ріс.44). описаний кут - кут, утворений двома дотичнимиAB і AC , Проведеними з однієї загальної точки ( BAC, рис.41).

довжина дуги кола пропорційна її радіусу r і відповідному центральному куті :

l \u003d r

Таким чином, якщо ми знаємо довжину дугиl і радіус r, То величина відповідного центрального кута

може бути визначена їх ставленням: \u003d L / r.

Ця формула є основою для визначення радіан вимірювання кутів. Так, якщо l = r,то \u003d 1, і ми говоримо, що кут дорівнює 1 радіану (це позначається: = 1 радий). Таким чином, ми маємо наступне визначення радіана як одиниці виміру кутів: радіан - це центральний кут ( AOB, рис.43), у якого довжина дуги дорівнює її радіусу (A mB \u003d AO, рис.43). Отже, радіанна міра будь-якого кута - це відношення довжини дуги, проведеної довільним радіусом і укладеної між сторонами цього кута, до її радіусу.Зокрема, відповідно до формули довжини дуги, довжина колаC може бути виражена таким чином:

де визначається як відношенняC до діаметру кола 2r :

= C /2 r.

ірраціональне число; його наближене значення 3.1415926…

З іншого боку, 2- це кругової кут кола, який в градусної системі вимірювання дорівнює 360º. На практиці часто трапляється, що як радіус дуги, так і кут невідомі. У цьому випадку довжина дуги може бути обчислена за наближеною формулою Гюйгенса:

p 2l + (2l - L) / 3 ,

де (див. ріс.42): p - довжина дуги ACB; l - довжина хорди AC; L - довжина хорди AB. Якщо дуга містить не більше ніж 60º , Відносна похибка цієї формули не перевищує 0.5%.

Співвідношення між елементами кола. вписаний кут ( ABC, Рис.45) дорівнює половині центрального кута , спирається на ту ж дугу A mC ( AOC, Рис.45) . Тому, всі вписані кути(Рис.45), спираються на одну і ту ж дугу (A mC , Рис.45), рівні.А так як центральний кут містить теж кількість градусів, щоі його дуга ( A mC , Рис.45), то будь-який вписаний кут вимірюється половиною дуги, на яку він спирається(у нашому випадку A mC).

Всі вписані кути, що спираються на півколо (APB, AQB, ..., ріс.46), прямі (Доведіть це, будь ласка!).

кут(AOD, ріс.47 ), Утворений двома хордами(ABі CD), вимірює ся напівсумою дуг, укладених між його сторонами: (A nD + C mB) / 2.

кут(AOD, рис.48) , утворений двома січними (AOі OD ), вимірюється Полуразность дуг, укладених між його сторонами: (A nD- B mC ) / 2. січною(COі BO ), вимірюється полуразность дуг, укладених між його сторонами: (B mC – C nD ) / 2 .

описаний кут(AOC, ріс.50 ), Утворений двома дотичними(COі AO ), вимірюється Полуразность дуг, укладених між його сторонами: (ABC – CDA) / 2 .

Твори відрізків хорд (AB і CD , Ріс.51 або рис.52), на які вони поділяються точкою перетину, рівні: AO · BO \u003d CO · DO.

До вадрат дотичній дорівнює добутку січної на її зовнішню частину (Ріс.50): OA 2 \u003d OB · O D (Доведіть!). Це властивість можна розглядати як окремий випадок рис.52.

хорда(AB , Рис.53) , Перпендикулярна діаметру(CD ), Ділиться в їх точці перетину O навпіл:AO \u003d OB.

( Спробуйте довести це!).

Що володіють деяким властивістю.

енциклопедичний YouTube

1 / 3

✪ Визначення параболи як ГМТ

✪ 124. Завдання на поверхні другого порядку. Геометричне місце точок

✪ Опір матеріалів. Лекція 21 (тензор напружень, головні напруження)

субтитри

Вітаю, дорогі друзі! Ми зараз будемо з вами займатися геометрією, а потім алгеброю, а потім все змішаємо і назвемо це математикою. Дуже просте питання. Уявіть собі, що там, де я поставив білу точку, грає музика (одна колонка). А потім з'явився технік і поставив колонку ще й на місце рожевої точки. Причому відстань між ними досить велика. Якщо ви встанете в зелений хрестик, то для вас музика буде доноситися з двох місць з затримкою. З одного з більшою затримкою, ніж з іншого. Як би встати так, щоб чути музику лівим і правим вухом зовсім однаково, синхронно? Тобто встати на рівних відстанях від двох колонок. Відповідь дуже проста, ви, звичайно, знаєте, якщо ходили хоча б в 7 клас. А якщо не ходили, можете здогадатися інтуїтивно. Треба побудувати відрізок, що з'єднує рожеву і білу точки, і в його центрі (в його серединці) зобразити перпендикуляр. Тоді будь-яка точка вертикального на цій дошці перпендикуляра однаково віддалена від рожевої і від білої. Чому так? Дуже просто. Тут два однакових трикутника. Чому вони однакові? Тому що у них є спільна сторона, ще дві сторони відзначені рівними штрихами. І прямі кути теж, звичайно, рівні один одному. Як наслідок, ми маємо право поставити рівні позначки на таких сторонах. Отже, ми з вами намалювали геометричне місце точок, однаково віддалених від двох заданих точок. А як щодо двох прямих? Давайте намалюємо пару прямих. Я намалюю дві паралельні прямі для початку. Це два берега і ви хочете плисти (з якоїсь причини) на рівних удалениях від цих двох берегів. Як побудувати цю траєкторію? Давайте знову побудуємо перпендикуляр до двох паралельних прямих. Знайдемо його серединку. А далі, озброївшись окоміром, намагаємося зобразити зелену лінію паралельно цим двом берегів. Звичайно, якщо ми візьмемо будь-яку точку на цій зеленій лінії і опустимо перпендикуляр на який-небудь берег, то ми можемо побачити прямокутник. А значить, ці сторони будуть рівні. Прямі можуть і перетинатися. І тоді ви теж легко вирішите таке завдання: безліч точок, однаково віддалених від цих двох прямих - це пара біссектрісс. Всі ці рішення будуються циркулем і лінійкою і зовсім легко проходяться на геометрії. А зараз я вам запропоную ще одне безліч, яке задається не двома однаковими об'єктами, а один об'єкт ми візьмемо з першого завдання: десь стоїть крапка, а інший об'єкт - з другої: є пряма. Причому ця точка нам потрібна надовго, тому ми введемо їй персональне ім'я: ми скажемо, що це точка F. Пряма теж персоналізована і називається буквою d. Уявіть собі на мить, що це межа пляжу: вище пляж, а нижче море. А точка F - це, наприклад, кіоск з морозивом. І ви хочете сісти так, щоб до кіоску з морозивом і до берега було рівну відстань. Тоді приклад такого місця цілком очевидна: точно так же, як і тут, і тут, ми будуємо перпендикуляр з точки F на пряму d, знаходимо його серединку і ось це саме виграшне місце: вам до кіоску дуже мало йти і до моря дуже мало йти . А як по-іншому можна сісти, щоб теж була однакова відстань і до кіоску, і до берега моря? Ось приклад ще один. Якщо ми побудуємо квадрат з такою стороною, то тоді рівність цих сторін і перпендикуляр тут теж нам гарантують, що ця точка годиться. Причому ясно, що раз пряжі простягається в обидві сторони, то і тут ми можемо намалювати такий же квадрат. Рішення буде симетрично. Давайте запишемо рішення для такого завдання. Ми шукаємо ось що: нам потрібно безліч букв М (точок, позначених буквою М), а умова на них ось яке: (ось ця годиться бути буквою М) відстань від будь-якої точки з цієї множини до F дорівнює ... Замість слова "відстань "я зараз напишу букву" ро ", тому що я хочу відстань від точки М до прямої d. Оскільки ми шукаємо безліч, тут стоять фігурні дужки. І ми шукаємо всі такі точки, позначені літерою М, щоб виконувалася ця рівність. Дві ми вже знайшли. Я маю право обвести цю точку зеленим кружечком і цю теж. Чи є хоча б одна точка між ними, яка належить цій безлічі? Однаково віддалена і від F, і від d. Так є. Давайте спробуємо зробити наступне. Зробимо крок на якусь величину вліво від відомої нам точки з множини. Питання: тоді ми отримаємо точку з цього ж безлічі? Подивимося на цю фігурку, на цей чотирикутник. Це прямокутник, тому тут теж допустимо один штрих. Відстань від отриманої точки до F як пов'язане з цим відрізком? Звичайно, воно більше, тут не можна поставити один штрих, тому що такий похилий відрізок - це гіпотінуза в трикутнику, де катет відзначений одним штрихом. Ця точка занадто низько, занадто близька до прямої d. Значить, треба її трошки підняти. Підняти настільки, щоб вона досить пішла від d і трошки наблизилася до F. Як саме - поки не будемо з'ясовувати, але це можливо. Ідея така: рухаючись вліво і піднімаючись вгору, ми можемо отримувати точки, що належать безлічі М. І якщо ще допустити, що крок може бути як завгодно маленьким, тоді зрозуміємо, що безліч це безперервно: це лінія, яку можна намалювати рухом руки, не зупиняючись і ніде не перестрибуючи. І ще ми знаємо, що лінія симетрична. Ця зелена лінія є зображенням цієї множини, позначеного фігурними дужками. Виявляється, це парабола. Це геометричне визначення для параболи. І тут починаються проблеми.