Przykład macierzy odwrotnej drugiego rzędu. Odwrotna macierz online

Cel usługi. Za pomocą tej usługi online można znaleźć dopełnienia algebraiczne, macierz transponowaną AT, macierz sprzężoną i macierz odwrotną.

Kalkulator online. Macierz odwrotna.

Rozwiązanie realizowane jest bezpośrednio na stronie (online) i jest bezpłatne. Wyniki obliczeń prezentowane są w raporcie Word oraz w formacie Excel (tzn. istnieje możliwość sprawdzenia rozwiązania). patrz przykład projektu.

Określ, czy macierz jest kwadratowa. Jeśli nie wtedy odwrotna macierz dla niej nie istnieje.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Uzupełnienia algebraiczne.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Następnie odwrotna macierz można zapisać jako:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Znajdowanie macierzy odwrotnej

Macierz А-1 nazywana jest macierzą odwrotną w stosunku do macierzy, jeśli А * А-1 =, gdzie jest macierzą jednostkową rzędu. Macierz odwrotna może istnieć tylko dla macierzy kwadratowych.

zobacz także Macierz odwrotna metodą Jordana-Gaussa

Algorytm znajdowania macierzy odwrotnej

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Znalezienie transponowanej macierzy AT.
Definicja dopełnień algebraicznych. Zastąp każdy element macierzy jego uzupełnieniem algebraicznym.
Składanie macierzy odwrotnej z dodawania algebraicznego: każdy element wynikowej macierzy jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Poniższy algorytm znajdowania macierzy odwrotnej jest podobny do poprzedniego, z wyjątkiem kilku kroków: najpierw obliczane są uzupełnienia algebraiczne, a następnie określana jest macierz sumy.

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Definicja dopełnień algebraicznych.
Wypełnienie macierzy sumarycznej (odwrotnościowej, sprzężonej).
Składanie macierzy odwrotnej z dopełnień algebraicznych: każdy element macierzy sprzężonej jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Przykład 1. Zapiszmy macierz w następujący sposób:

Macierz odwrotna istnieje, jeśli wyznacznik macierzy jest niezerowy. Znajdź wyznacznik macierzy:
= -1 (-1 4 - (- 2 5)) - 2 (2 4 - (- 2 (-2))) + 3 (2 5 - (- 1 (-2))) = 10. Wyznacznikiem jest 10 i nie jest równe zeru. Kontynuujemy rozwiązanie.
Znajdź transponowaną macierz:
Uzupełnienia algebraiczne.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Następnie odwrotna macierz można zapisać jako:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Kolejny algorytm znajdowania macierzy odwrotnej

Podajmy inny schemat znajdowania macierzy odwrotnej.

Znajdź wyznacznik danej macierzy kwadratowej.
Znajdź algebraiczne dopełnienia wszystkich elementów macierzy.
Dopełnienia algebraiczne elementów wierszowych zapisujemy w kolumnach (transpozycja).
Każdy element wynikowej macierzy dzielimy przez wyznacznik macierzy.

Jak widać, operację transpozycji można zastosować zarówno na początku, na oryginalnej macierzy, jak i na końcu, na otrzymanych uzupełnieniach algebraicznych.

Przypadek szczególny: Odwrotnością macierzy tożsamości jest macierz tożsamości.

Przykład nr 2. Znajdź odwrotność macierzy .
Rozwiązanie.
1. Znajdź
.
2. Poszukujemy dopełnień algebraicznych każdego elementu macierzy A:
; ; .
Otrzymaliśmy algebraiczne dodatki elementów pierwszego wiersza.

Znajdź odwrotną macierz online

Podobnie dla elementów drugiej i trzeciej linii otrzymujemy:
; ; .
; ; .
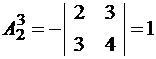Łącząc punkty 3 i 4 otrzymujemy macierz odwrotną

.
Aby to sprawdzić, upewnij się, że A-1A = E.

Instrukcja. Aby uzyskać rozwiązanie, konieczne jest ustawienie wymiaru matrycy. Następnie w nowym oknie dialogowym wypełnij macierz.

Znajdowanie macierzy odwrotnej

Macierz А-1 nazywana jest macierzą odwrotną w stosunku do macierzy, jeśli А * А-1 =, gdzie jest macierzą jednostkową rzędu. Macierz odwrotna może istnieć tylko dla macierzy kwadratowych.

Cel usługi. Za pomocą tej usługi online można znaleźć dopełnienia algebraiczne, macierz transponowaną AT, macierz sprzężoną i macierz odwrotną. Rozwiązanie realizowane jest bezpośrednio na stronie (online) i jest bezpłatne. Wyniki obliczeń prezentowane są w raporcie Word oraz w formacie Excel (tzn. istnieje możliwość sprawdzenia rozwiązania). patrz przykład projektu.

Znajdowanie odwrotnej macierzy online

zobacz także Macierz odwrotna metodą Jordana-Gaussa

Algorytm znajdowania macierzy odwrotnej

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Znalezienie transponowanej macierzy AT.
Definicja dopełnień algebraicznych. Zastąp każdy element macierzy jego uzupełnieniem algebraicznym.
Składanie macierzy odwrotnej z dodawania algebraicznego: każdy element wynikowej macierzy jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Definicja dopełnień algebraicznych.
Wypełnienie macierzy sumarycznej (odwrotnościowej, sprzężonej).
Składanie macierzy odwrotnej z dopełnień algebraicznych: każdy element macierzy sprzężonej jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Przykład 1. Zapiszmy macierz w następujący sposób:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Następnie odwrotna macierz można zapisać jako:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Kolejny algorytm znajdowania macierzy odwrotnej

Podajmy inny schemat znajdowania macierzy odwrotnej.

Znajdź wyznacznik danej macierzy kwadratowej.
Znajdź algebraiczne dopełnienia wszystkich elementów macierzy.
Dopełnienia algebraiczne elementów wierszowych zapisujemy w kolumnach (transpozycja).
Każdy element wynikowej macierzy dzielimy przez wyznacznik macierzy.

Jak widać, operację transpozycji można zastosować zarówno na początku, na oryginalnej macierzy, jak i na końcu, na otrzymanych uzupełnieniach algebraicznych.

Aby to sprawdzić, upewnij się, że A-1A = E.

Instrukcja. Aby uzyskać rozwiązanie, konieczne jest ustawienie wymiaru matrycy. Następnie w nowym oknie dialogowym wypełnij macierz.

Znalezienie macierzy odwrotnej jest ważną częścią sekcji algebry liniowej. Przy pomocy takich matryc, jeśli istnieją, można szybko znaleźć rozwiązanie dla systemu równania liniowe.

Macierz nazywa się odwrotnością macierzy, jeśli spełnione są następujące równości.

Jeśli wyznacznik macierzy jest niezerowy, wówczas macierz nazywa się nieszczególną lub niezdegenerowaną.

Aby macierz miała odwrotność, konieczne i wystarczające jest, aby była niezdegenerowana

Algorytm znajdowania macierzy odwrotnej

Niech mamy macierz kwadratową

i musisz znaleźć coś przeciwnego. Aby to zrobić, wykonaj następujące kroki:

1. Znajdź wyznacznik macierzy. Jeśli nie jest równy zero, wykonujemy następujące czynności. Inaczej ta macierz jest zdegenerowana i dla niej nie ma odwrotności

2. Znajdź dopełnienia algebraiczne elementów macierzy. Są równe mnożnikom pomnożonym przez potęgę sumy wiersza i kolumny, których szukamy.

3. Skonstruować macierz z dopełnień algebraicznych elementów macierzy tej macierzy i dokonać jej prototranspozycji. Ta matryca nazywana jest dołączoną lub sprzymierzoną i oznaczona.

4. Podziel załączoną macierz na wyznaczniki. Otrzymana macierz będzie odwrotna i będzie miała właściwości opisane na początku artykułu.

Znajdź macierz odwrotną do macierzy (Dubovik V.P., Yurik I.I.

Znajdowanie macierzy odwrotnej

„Wyższa matematyka. Zbiór problemów”)

1) Znajdź wyznacznik macierzy

Ponieważ wyznacznikiem nie jest zero (), macierz odwrotna istnieje. Znajdź macierz złożoną z dopełnień algebraicznych

Macierz dopełnienia przyjmie postać

Transponujemy to i dostajemy załącznik

Dzielimy to przez wyznacznik i otrzymujemy odwrotność

Widzimy to w przypadku, gdy wyznacznik jest równy jeden sprzężone i odwrotne macierze są takie same.

2) Oblicz wyznacznik macierzy

Znajdź macierz dopełnień algebraicznych

Ostateczna forma macierzy dopełnienia

Transponujemy to i znajdujemy macierz unii

Znajdź macierz odwrotną

3) Obliczmy wyznacznik macierzy. Aby to zrobić, rozwiń go do pierwszej linii. W rezultacie otrzymujemy dwa niezerowe wyrazy

Znajdź macierz dopełnień algebraicznych. Harmonogram wyznacznika realizowany jest w wierszach i kolumnach, w których jest więcej elementów zerowych (zaznaczonych na czarno).

Ostateczna postać macierzy dopełniacza jest następująca.

Transponujemy to i znajdujemy powiązaną macierz

Ponieważ wyznacznik macierzy jest równy jeden, macierz odwrotna pokrywa się z sąsiednią. Ten przykład Powrót.

Podczas obliczania macierzy odwrotnej typowe są błędy związane z nieprawidłowymi znakami podczas obliczania wyznacznika i macierzy dopełnienia.

Matematyka wyższa »Macierze i wyznaczniki» Macierz odwrotna »Obliczanie macierzy odwrotnej za pomocą dodawania algebraicznego.

Algorytm obliczania macierzy odwrotnej za pomocą uzupełnień algebraicznych: metoda macierzy sprzężonych (sprzężonych).

Macierz $ A ^ (- 1) $ nazywana jest odwrotną w stosunku do macierzy kwadratowej $ A $, jeśli spełniony jest warunek $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ , gdzie $ E $ Jest macierzą jednostkową, której kolejność jest równa kolejności macierzy $ A $.

Macierz niezdegenerowana - macierz, której wyznacznik nie jest równy zero. W związku z tym zdegenerowana macierz to taka, dla której wyznacznik jest równy zero.

Macierz odwrotna $ A ^ (- 1) $ istnieje wtedy i tylko wtedy, gdy macierz $ A $ jest niezdegenerowana. Jeżeli macierz odwrotna $ A ^ (- 1) $ istnieje, to jest unikalna.

Istnieje kilka sposobów na znalezienie odwrotności macierzy, a my przyjrzymy się dwóm z nich. Na tej stronie zostanie omówiona metoda matrycy sprzężonej, która jest uważana za standardową w większości kursów. wyższa matematyka... W drugiej części omówiono drugą metodę znajdowania macierzy odwrotnej (metoda przekształceń elementarnych), która polega na wykorzystaniu metody Gaussa lub metody Gaussa-Jordana.

Metoda macierzy sprzężonej (sprzężonej)

Niech zostanie podana macierz $ A_ (n \ razy n) $. Aby znaleźć odwrotność $ A ^ (- 1) $, wymagane są trzy kroki:

Znajdź wyznacznik macierzy $ A $ i upewnij się, że $ \ Delta A \ neq 0 $, tj. że macierz A jest niezdegenerowana.
Uzupełnij algebraiczne $ A_ (ij) $ każdego elementu macierzy $ A $ i zapisz macierz $ A_ (n \ razy n) ^ (*) = \ left (A_ (ij) \ right) $ z znaleziono dopełnienia algebraiczne.
Napisz macierz odwrotną, biorąc pod uwagę wzór $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Macierz $ (A ^ (*)) ^ T $ jest często określana jako sprzężona (odwrotnie, sprzężona) z macierzą $ A $.

Jeżeli rozwiązanie jest wykonywane ręcznie, to pierwsza metoda jest dobra tylko dla macierzy o stosunkowo małych rzędach: druga (przykład nr 2), trzecia (przykład nr 3), czwarta (przykład nr 4). Aby znaleźć odwrotność macierzy wyższy porządek, stosowane są inne metody. Na przykład metoda Gaussa, o której mowa w drugiej części.

Przykład 1

Znajdź odwrotność $ A = \ lewo (\ początek (tablica) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 i -9 i 0 \ koniec (tablica) \ prawo) $.

odwrotna macierz

Ponieważ wszystkie elementy czwartej kolumny są równe zeru, to $ \ Delta A = 0 $ (czyli macierz $ A $ jest zdegenerowana). Ponieważ $ \ Delta A = 0 $, macierz odwrotna do macierzy $ A $ nie istnieje.

Przykład nr 2

Znajdź odwrotność macierzy $ A = \ left (\ begin (tablica) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $.

Używamy metody sprzężonej macierzy. Najpierw znajdujemy wyznacznik danej macierzy $ A $:

$$ \ Delta A = \ lewo | \ begin (tablica) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Ponieważ $ \ Delta A \ neq 0 $, to macierz odwrotna istnieje, dlatego będziemy kontynuować rozwiązanie. Znajdujemy dopełnienia algebraiczne każdego elementu danej macierzy:

\ początek (wyrównane) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ koniec (wyrównany)

Tworzymy macierz z dopełnień algebraicznych: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Transponuj wynikową macierz: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (wynikowa macierz jest często określana jako macierz sprzężona lub macierz sprzężona z macierzą $A $). Korzystając ze wzoru $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, mamy:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (tablica) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (tablica) \ right) $$

Zatem odwrotność jest znaleziona: $ A ^ (- 1) = \ left (\ begin (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. Aby sprawdzić prawdziwość wyniku wystarczy sprawdzić prawdziwość jednej z równości: $ A ^ (- 1) \ cdot A = E $ lub $ A \ cdot A ^ (- 1) = E $. Sprawdźmy równość $ A ^ (- 1) \ cdot A = E $. Aby mniej pracować z ułamkami, podstawimy macierz $ A ^ (- 1) $ nie w postaci $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, a jako $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ koniec (tablica ) \ prawo) $:

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ koniec (tablica) \ prawo) $.

Przykład nr 3

Znajdź odwrotność macierzy $ A = \ left (\ begin (tablica) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $.

Zacznijmy od obliczenia wyznacznika macierzy $A $. Zatem wyznacznik macierzy $ A $ jest następujący:

$$ \ Delta A = \ lewo | \ begin (tablica) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (tablica) \ right | = 18-36 + 56-12 = 26. $$

Ponieważ $ \ Delta A \ neq 0 $, to macierz odwrotna istnieje, dlatego będziemy kontynuować rozwiązanie. Znajdujemy dopełnienia algebraiczne każdego elementu danej macierzy:

Komponujemy macierz dopełnień algebraicznych i transponujemy ją:

$$ A ^ * = \ lewo (\ begin (tablica) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (tablica) \ right); \; (A ^ *) ^ T = \ lewo (\ początek (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (tablica) \ prawo) $$

Korzystając ze wzoru $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, otrzymujemy:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (tablica) \ right) = \ left (\ begin (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ koniec (tablica) \ prawo) $$

Czyli $ A ^ (- 1) = \ lewo (\ początek (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 i -3/26 i 37/26 \ koniec (tablica) \ prawo) $. Aby sprawdzić prawdziwość wyniku wystarczy sprawdzić prawdziwość jednej z równości: $ A ^ (- 1) \ cdot A = E $ lub $ A \ cdot A ^ (- 1) = E $. Sprawdźmy równość $ A \ cdot A ^ (- 1) = E $. Aby mniej pracować z ułamkami, podstawimy macierz $ A ^ (- 1) $ not w postaci $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $ i jako $ \ frac (1) (26) \ cdot \ left ( \ begin (tablica) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

Sprawdzenie powiodło się, odwrotność $ A ^ (- 1) $ została znaleziona poprawnie.

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 i -3/26 i 37/26 \ koniec (tablica) \ prawo) $.

Przykład nr 4

Znajdź odwrotność $ A = \ lewo (\ początek (tablica) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ koniec (tablica) \ prawo) $.

W przypadku macierzy czwartego rzędu znalezienie macierzy odwrotnej przy użyciu uzupełnień algebraicznych jest nieco trudne. Jednak takie przykłady można znaleźć w pracach testowych.

Aby znaleźć odwrotność macierzy, należy najpierw obliczyć wyznacznik macierzy $ A $. Najlepszym sposobem na zrobienie tego w tej sytuacji jest rozwinięcie wyznacznika o wiersz (kolumnę). Wybieramy dowolny wiersz lub kolumnę i znajdujemy algebraiczne dopełnienia każdego elementu wybranego wiersza lub kolumny.

Na przykład dla pierwszej linii otrzymujemy:

Wyznacznik macierzy $A $ jest obliczany według następującego wzoru:

$$ \ Delta A = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

Algebraiczna Macierz Dopełnień: $ A ^ * = \ left (\ begin (tablica) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ koniec (tablica) \ prawo) $.

Macierz sprzężona: $ (A ^ *) ^ T = \ left (\ begin (tablica) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 i -463 \\ -112 i 4 i 36 i -96 \ koniec (tablica) \ prawo) $

Macierz odwrotna:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ begin (tablica) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (tablica) \ right) = \ left (\ begin (tablica) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 i 1/25 i 9/25 i -24/25 \ koniec (tablica) \ prawo) $$

Badanie:

W związku z tym macierz odwrotna została znaleziona poprawnie.

Odpowiedź: $ A ^ (- 1) = \ lewo (\ początek (tablica) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ koniec (tablica) \ prawo ) $.

W drugiej części zostanie rozważony inny sposób znajdowania macierzy odwrotnej, który polega na wykorzystaniu przekształceń metody Gaussa lub metody Gaussa-Jordana.

Zajęcia online z matematyki wyższej

Znajdowanie macierzy odwrotnej

Macierz А-1 nazywana jest macierzą odwrotną w stosunku do macierzy, jeśli А * А-1 =, gdzie jest macierzą jednostkową rzędu. Macierz odwrotna może istnieć tylko dla macierzy kwadratowych.

zobacz także Macierz odwrotna metodą Jordana-Gaussa

Algorytm znajdowania macierzy odwrotnej

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Znalezienie transponowanej macierzy AT.
Definicja dopełnień algebraicznych. Zastąp każdy element macierzy jego uzupełnieniem algebraicznym.
Składanie macierzy odwrotnej z dodawania algebraicznego: każdy element wynikowej macierzy jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Definicja dopełnień algebraicznych.
Wypełnienie macierzy sumarycznej (odwrotnościowej, sprzężonej).
Składanie macierzy odwrotnej z dopełnień algebraicznych: każdy element macierzy sprzężonej jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Przykład 1. Zapiszmy macierz w następujący sposób:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Następnie odwrotna macierz można zapisać jako:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Kolejny algorytm znajdowania macierzy odwrotnej

Podajmy inny schemat znajdowania macierzy odwrotnej.

Znajdź wyznacznik danej macierzy kwadratowej.
Znajdź algebraiczne dopełnienia wszystkich elementów macierzy.
Dopełnienia algebraiczne elementów wierszowych zapisujemy w kolumnach (transpozycja).
Każdy element wynikowej macierzy dzielimy przez wyznacznik macierzy.

Jak widać, operację transpozycji można zastosować zarówno na początku, na oryginalnej macierzy, jak i na końcu, na otrzymanych uzupełnieniach algebraicznych.

Aby to sprawdzić, upewnij się, że A-1A = E.

Instrukcja. Aby uzyskać rozwiązanie, konieczne jest ustawienie wymiaru matrycy. Następnie w nowym oknie dialogowym wypełnij macierz.

Macierz A -1 nazywana jest macierzą odwrotną w stosunku do macierzy A, jeśli A * A -1 = E, gdzie E jest macierzą jednostkową n-tego rzędu. Macierz odwrotna może istnieć tylko dla macierzy kwadratowych.

Cel usługi... Za pomocą tej usługi online można znaleźć dopełnienia algebraiczne, macierz transponowaną AT, macierz sprzężoną i macierz odwrotną. Rozwiązanie realizowane jest bezpośrednio na stronie (online) i jest bezpłatne. Wyniki obliczeń prezentowane są w raporcie Word oraz w formacie Excel (tzn. istnieje możliwość sprawdzenia rozwiązania). patrz przykład projektu.

Instrukcja. Aby uzyskać rozwiązanie, konieczne jest ustawienie wymiaru matrycy. Następnie w nowym oknie dialogowym wypełnij macierz A.

Zobacz także Macierz odwrotna przy użyciu metody Jordana-Gaussa

Algorytm znajdowania macierzy odwrotnej

Znalezienie transponowanej macierzy AT.
Definicja dopełnień algebraicznych. Zastąp każdy element macierzy jego uzupełnieniem algebraicznym.
Składanie macierzy odwrotnej z dodawania algebraicznego: każdy element wynikowej macierzy jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.

Następny algorytm macierzy odwrotnej jest podobny do poprzedniego, z wyjątkiem kilku kroków: najpierw obliczane są uzupełnienia algebraiczne, a następnie wyznaczana jest macierz sprzężona C.

Określ, czy macierz jest kwadratowa. Jeśli nie, to nie ma dla niego macierzy odwrotnej.
Obliczanie wyznacznika macierzy A. Jeśli nie jest równe zero, kontynuujemy rozwiązanie, w przeciwnym razie macierz odwrotna nie istnieje.
Definicja dopełnień algebraicznych.
Wypełnienie macierzy sumarycznej (odwrotnościowej, sprzężonej) C.
Składanie macierzy odwrotnej z dopełnień algebraicznych: każdy element macierzy sprzężonej C jest podzielony przez wyznacznik macierzy pierwotnej. Otrzymana macierz jest odwrotnością macierzy oryginalnej.
Przeprowadzana jest kontrola: macierze pierwotna i wynikowa są mnożone. Wynikiem powinna być macierz tożsamości.

Przykład 1. Zapiszmy macierz w następujący sposób:

Uzupełnienia algebraiczne. ∆ 1,2 = - (2 4 - (- 2 (-2))) = -4 ∆ 2,1 = - (2 4-5 3) = 7 ∆ 2,3 = - (- 1 5 - (- 2 2)) = 1 ∆ 3,2 = - (- 1 (-2) -2 3) = 4

A -1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Kolejny algorytm znajdowania macierzy odwrotnej

Podajmy inny schemat znajdowania macierzy odwrotnej.

Znajdź wyznacznik danej macierzy kwadratowej A.
Znajdź algebraiczne dopełnienia wszystkich elementów macierzy A.
Dopełnienia algebraiczne elementów wierszowych zapisujemy w kolumnach (transpozycja).
Każdy element wynikowej macierzy dzielimy przez wyznacznik macierzy A.

Jak widać, operację transpozycji można zastosować zarówno na początku, na oryginalnej macierzy, jak i na końcu, na otrzymanych uzupełnieniach algebraicznych.

Szczególny przypadek: Odwrotnością macierzy jednostkowej E jest macierz jednostkowa E.

Kontynuujemy rozmowę o akcjach z macierzami. Mianowicie - w trakcie studiowania tego wykładu dowiesz się, jak znaleźć macierz odwrotną. Uczyć się. Nawet jeśli matematyka jest napięta.

Co to jest macierz odwrotna? Tutaj możesz narysować analogię z odwrotnością liczb: rozważ na przykład optymistyczną liczbę 5 i jej odwrotność. Iloczyn tych liczb jest równy jeden:. Z macierzami wszystko jest podobne! Iloczyn macierzy przez jej macierz odwrotną wynosi - macierz jednostkowa, który jest macierzowym odpowiednikiem jednostki numerycznej. Jednak najpierw rozwiążemy ważną kwestię praktyczną, a mianowicie dowiemy się, jak znaleźć tę bardzo odwrotną macierz.

Co musisz wiedzieć i umieć znaleźć, aby znaleźć macierz odwrotną? Musisz być w stanie się zdecydować wyznaczniki... Musisz zrozumieć, co to jest matryca i móc wykonywać z nimi pewne czynności.

Istnieją dwie główne metody znajdowania odwrotności macierzy:
przez dopełnienia algebraiczne oraz za pomocą przekształceń elementarnych.

Dzisiaj zbadamy pierwszy, łatwiejszy sposób.

Zacznijmy od najstraszniejszego i niezrozumiałego. Rozważać kwadrat matryca. Macierz odwrotną można znaleźć według następującego wzoru::

Gdzie jest wyznacznik macierzy, jest transponowaną macierzą algebraicznych uzupełnień odpowiednich elementów macierzy.

Pojęcie macierzy odwrotnej istnieje tylko dla macierzy kwadratowych, macierze „dwa na dwa”, „trzy na trzy” itp.

Oznaczenia: Jak pewnie już zauważyłeś, odwrotność macierzy jest oznaczona indeksem górnym

Zacznijmy od najprostszego przypadku - macierzy dwa na dwa. Najczęściej oczywiście wymagane jest „trzy na trzy”, ale mimo to zdecydowanie zalecam przestudiowanie prostszego zadania w celu opanowania ogólnej zasady rozwiązania.

Przykład:

Znajdź odwrotność macierzy

My decydujemy. Kolejność działań można wygodnie rozbić na punkty.

1) Najpierw znajdź wyznacznik macierzy.

Jeśli twoje zrozumienie tego działania nie jest wystarczająco dobre, przeczytaj materiał Jak obliczyć wyznacznik?

Ważny! W przypadku, gdy wyznacznikiem macierzy jest ZERO- macierz odwrotna NIE ISTNIEJE.

W rozważanym przykładzie, jak się okazało, oznacza to, że wszystko jest w porządku.

2) Znajdź macierz nieletnich.

Aby rozwiązać nasz problem, nie trzeba wiedzieć, kim jest nieletni, jednak warto zapoznać się z artykułem Jak obliczyć wyznacznik.

Macierz małoletnich ma takie same wymiary jak macierz, czyli w tym przypadku.
Sprawa jest niewielka, pozostaje znaleźć cztery liczby i umieścić je zamiast gwiazdek.

Powrót do naszej matrycy
Spójrzmy najpierw na lewy górny element:

Jak to znaleźć mniejszy?
Odbywa się to w ten sposób: ZAMYŚLNIE przekreśl wiersz i kolumnę, w której znajduje się ten element:

Pozostała liczba to drobne tego elementu, które wpisujemy do naszej macierzy nieletnich:

Rozważ następujący element macierzy:

W myślach przekreślamy wiersz i kolumnę, w których znajduje się ten element:

Pozostaje drobny element tego elementu, który zapisujemy w naszej macierzy:

Podobnie rozważamy elementy drugiej linii i znajdujemy ich podrzędne:

Gotowe.

To proste. W matrycy nieletnich potrzebujesz ZMIEŃ ZNAKI dwie liczby:

To są liczby, które zakreśliłem!

- macierz dopełnień algebraicznych odpowiednich elementów macierzy.

A to po prostu...

4) Znajdź transponowaną macierz dopełnień algebraicznych.

- transponowana macierz dopełnień algebraicznych odpowiednich elementów macierzy.

5) Odpowiedz.

Pamiętając o naszej formule
Wszystko zostało znalezione!

Czyli odwrotność macierzy to:

Odpowiedź najlepiej pozostawić taką, jaka jest. NIE MA POTRZEBY podziel każdy element macierzy przez 2, ponieważ otrzymujesz liczby ułamkowe. Ten niuans omówiono bardziej szczegółowo w tym samym artykule. Operacje na macierzach.

Jak mogę sprawdzić rozwiązanie?

Konieczne jest wykonanie mnożenia macierzy lub

Badanie:

Wspomniane już macierz jednostkowa Czy macierz z włączonymi jedynkami? główna przekątna i zera gdzie indziej.

Zatem odwrotność jest poprawna.

Jeśli wykonasz akcję, wynikiem będzie również macierz tożsamości. To jeden z nielicznych przypadków, w których mnożenie macierzy jest przemienne, więcej dokładna informacja można znaleźć w artykule Własności operacji na macierzach. Wyrażenia macierzowe... Zauważ też, że podczas sprawdzania stała (ułamek) jest przesuwana do przodu i przetwarzana na samym końcu - po mnożeniu macierzy. To jest standardowa technika.

Przejdźmy do bardziej powszechnego przypadku w praktyce - macierzy „trzy na trzy”:

Przykład:

Znajdź odwrotność macierzy

Algorytm jest dokładnie taki sam jak w przypadku dwa na dwa.

Macierz odwrotną znajdujemy według wzoru:, gdzie jest transponowaną macierzą dopełnień algebraicznych odpowiednich elementów macierzy.

1) Znajdź wyznacznik macierzy.

Tutaj ujawnia się wyznacznik w pierwszej linii.

Nie zapominaj też o tym, co oznacza, że wszystko jest w porządku - macierz odwrotna istnieje.

2) Znajdź macierz nieletnich.

Macierz małoletnich ma wymiar „trzy na trzy” i musimy znaleźć dziewięć liczb.

Omówię szczegółowo kilka drobnych szczegółów:

Rozważ następujący element macierzy:

MYŚLNIE przekreśl wiersz i kolumnę, w której znajduje się ten element:

Pozostałe cztery liczby są zapisywane w wyznaczniku „dwa na dwa”

Ten kwalifikator to „dwa na dwa” i jest drugorzędnym elementem tego elementu... Należy to obliczyć:

To tyle, nieletni zostaje znaleziony, zapisujemy to w naszej matrycy nieletnich:

Jak można się domyślić, należy obliczyć dziewięć wyznaczników dwa na dwa. Proces oczywiście jest ponury, ale sprawa nie jest najtrudniejsza, może być gorzej.

Cóż, żeby się skonsolidować - znalezienie kolejnego nieletniego na zdjęciach:

Spróbuj sam obliczyć resztę nieletnich.

Ostateczny wynik:
- macierz małoletnich odpowiednich elementów macierzy.

To, że wszyscy nieletni okazali się negatywni, to czysty przypadek.

3) Znajdź macierz dopełnień algebraicznych.

W matrycy nieletnich jest to konieczne ZMIEŃ ZNAKIściśle dla następujących elementów:

W tym przypadku:

Nie rozważamy znalezienia macierzy odwrotnej dla macierzy „cztery na cztery”, ponieważ takie zadanie może postawić tylko nauczyciel sadystyczny (aby uczeń obliczył jeden wyznacznik „cztery na cztery” i 16 wyznaczników „trzy na trzy” ). W swojej praktyce spotkałem się tylko z jednym takim przypadkiem, a klient praca testowa zapłaciłem za moją udrękę całkiem drogo =).

W wielu podręcznikach, podręcznikach można znaleźć nieco inne podejście do znajdowania macierzy odwrotnej, jednak polecam skorzystać z powyższego algorytmu rozwiązania. Czemu? Ponieważ prawdopodobieństwo pomyłki w obliczeniach i znakach jest znacznie mniejsze.

Ten temat jest jednym z najbardziej znienawidzonych wśród studentów. Gorsze są chyba tylko determinanty.

Sztuczka polega na tym, że samo pojęcie elementu odwrotnego (i nie mówię teraz tylko o macierzach) odsyła nas do operacji mnożenia. Nawet w program nauczania mnożenie jest uważane za operację złożoną, a mnożenie macierzy to generalnie osobny temat, któremu poświęciłem cały akapit i samouczek wideo.

Nie będziemy dziś wchodzić w szczegóły obliczeń macierzowych. Pamiętaj tylko: jak oznacza się macierze, jak się je mnoży i co z tego wynika.

Powtórzenie: mnożenie macierzy

Przede wszystkim uzgodnijmy notację. Macierz $ A $ o rozmiarze $ \ left [m \ razy n \ right] $ to po prostu tablica liczb, w której są dokładnie $ m $ wierszy i $ n $ kolumn:

\ = \ underbrace (\ left [\ begin (macierz) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) \\ ((( a) _ (21)) & ((a) _ (22)) & ... & ((a) _ (2n)) \\ ... & ... & ... & ... \\ ((a) _ (m1)) & ((a) _ (m2)) & ... & ((a) _ (mn)) \\\ end (matryca) \ prawo]) _ (n) \]

Aby przypadkowo nie pomylić wierszy i kolumn w miejscach (uwierz mi, możesz pomylić 1 z 2 na egzaminie - co możemy powiedzieć o niektórych wierszach), spójrz na zdjęcie:

Wyznaczanie wskaźników dla komórek macierzy

Co się dzieje? Jeśli umieścisz standardowy układ współrzędnych $ OXY $ w lewym górnym rogu i skierujesz osie tak, aby obejmowały całą macierz, to każda komórka tej macierzy może być jednoznacznie powiązana ze współrzędnymi $\lewo (x;y\prawo) $ - będzie to numer wiersza i numer kolumny.

Dlaczego układ współrzędnych znajduje się w lewym górnym rogu? Bo to właśnie stamtąd zaczynamy czytać dowolne teksty. Bardzo łatwo to zapamiętać.

Dlaczego oś $ x $ jest skierowana w dół, a nie w prawo? Znowu wszystko jest proste: weź standardowy układ współrzędnych (oś $ x $ idzie w prawo, oś $ y $ idzie w górę) i obróć go tak, aby obejmował macierz. Jest to obrót o 90 stopni w kierunku zgodnym z ruchem wskazówek zegara - możemy zobaczyć jego wynik na zdjęciu.

Ogólnie rzecz biorąc, zorientowaliśmy się, jak określić indeksy elementów macierzy. Zajmijmy się teraz mnożeniem.

Definicja. Macierze $ A = \ lewo [m \ razy n \ prawo] $ i $ B = \ lewo [n \ razy k \ prawo] $, gdy liczba kolumn w pierwszej jest taka sama jak liczba wierszy w drugiej , nazywane są spójnymi.

W tej kolejności. Można się pomylić i powiedzieć, jak mówią, macierze $ A $ i $ B $ tworzą uporządkowaną parę $ \ lewo (A; B \ prawo) $: jeśli są zgodne w tej kolejności, to zupełnie niepotrzebne jest, aby $ B $ i $ A $, te. para $ \ lewa (B; A \ prawa) $ jest również dopasowana.

Tylko pasujące macierze mogą być mnożone.

Definicja. Iloczyn dopasowanych macierzy $ A = \ lewo [m \ razy n \ prawo] $ i $ B = \ lewo [n \ razy k \ prawo] $ jest nową macierzą $ C = \ lewo [m \ razy k \ prawo ] $ , którego elementy $ ((c) _ (ij)) $ obliczamy według wzoru:

\ [((c) _ (ij)) = \ suma \ limity_ (k = 1) ^ (n) (((a) _ (ik))) \ cdot ((b) _ (kj)) \]

Innymi słowy: aby uzyskać element $ ((c) _ (ij)) $ macierzy $ C = A \ cdot B $, musisz wziąć wiersz $ i $ pierwszej macierzy, $ j $ -tej kolumny drugiej macierzy, a następnie pomnóż parami elementy z tego wiersza i kolumny. Zsumuj wyniki.

Tak, to bardzo surowa definicja. Od razu wynika z tego kilka faktów:

Ogólnie rzecz biorąc, mnożenie macierzy jest nieprzemienne: $ A \ cdot B \ ne B \ cdot A $;
Jednak mnożenie jest asocjacyjne: $ \ left (A \ cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ right) $;
A nawet dystrybucyjnie: $ \ lewo (A + B \ prawo) \ cdot C = A \ cdot C + B \ cdot C $;
I znowu rozdzielczo: $ A \ cdot \ lewo (B + C \ prawo) = A \ cdot B + A \ cdot C $.

Rozdzielczość mnożenia musiała być opisana oddzielnie dla lewego i prawego sumy mnożnika, właśnie ze względu na nieprzemienność operacji mnożenia.

Jeśli jednak okaże się, że $ A \ cdot B = B \ cdot A $, takie macierze nazywamy macierzami permutacyjnymi.

Wśród wszystkich macierzy, które są tam pomnożone przez coś, są specjalne - takie, które po pomnożeniu przez dowolną macierz $A $, znowu dają $A $:

Definicja. Macierz $E $ nazywana jest tożsamością, jeśli $ A \ cdot E = A $ lub $ E \ cdot A = A $. W przypadku macierzy kwadratowej $ A $ możemy napisać:

Macierz jednostkowa jest częstym gościem przy rozwiązywaniu równań macierzowych. I w ogóle częsty gość w świecie matryc :)

A także z powodu tego $E $, ktoś wymyślił całą grę, która zostanie napisana dalej.

Co to jest macierz odwrotna

Ponieważ mnożenie macierzy jest bardzo czasochłonną operacją (trzeba pomnożyć kilka wierszy i kolumn), koncepcja macierzy odwrotnej również nie należy do najbanalniejszych. I wymagajace wyjasnienia.

Definicja klucza

Cóż, czas poznać prawdę.

Definicja. Macierz $ B $ nazywana jest odwrotnością macierzy $ A $ if

Macierz odwrotna jest oznaczona przez $ ((A) ^ (- 1)) $ (nie mylić ze stopniem!), więc definicję można przepisać w następujący sposób:

Wydawałoby się, że wszystko jest niezwykle proste i jasne. Ale analizując taką definicję, od razu pojawia się kilka pytań:

Czy macierz odwrotna zawsze istnieje? A jeśli nie zawsze, to jak ustalić: kiedy istnieje, a kiedy nie?
A kto powiedział, że jest dokładnie jedna taka matryca? A co jeśli dla jakiejś macierzy początkowej $ A $ istnieje cała masa odwrotnych macierzy?
Jak wyglądają te wszystkie rewersy? A jak właściwie mają być liczone?

Jeśli chodzi o algorytmy obliczeniowe - o tym porozmawiamy nieco później. Ale na pozostałe pytania odpowiemy już teraz. Sformułujmy je w formie oddzielnych stwierdzeń-lematów.

Podstawowe właściwości

Zacznijmy od tego, jak powinna wyglądać macierz $ A $, aby miała $ ((A) ^ (- 1)) $. Teraz upewnimy się, że obie te macierze muszą być kwadratowe i tej samej wielkości: $ \ left [n \ razy n \ right] $.

Lemat 1. Mając macierz $ A $ i jej odwrotność $ ((A) ^ (- 1)) $. Wtedy obie te macierze są kwadratowe, z tym samym porządkiem $ n $.

Dowód. To proste. Niech macierz $ A = \ lewo [m \ razy n \ prawo] $, $ ((A) ^ (- 1)) = \ lewo [a \ razy b \ prawo] $. Ponieważ iloczyn $ A \ cdot ((A) ^ (- 1)) = E $ istnieje z definicji, macierze $ A $ i $ ((A) ^ (- 1)) $ są dopasowywane we wskazanej kolejności:

\ [\ początek (wyrównaj) & \ lewo [m \ razy n \ prawo] \ cdot \ lewo [a \ razy b \ prawo] = \ lewo [m \ razy b \ prawo] \\ & n = a \ koniec ( wyrównywać) \]

Jest to bezpośrednia konsekwencja algorytmu mnożenia macierzy: współczynniki $ n $ i $ a $ są „przejściowe” i muszą być równe.

Jednocześnie definiuje się również mnożenie odwrotne: $ ((A) ^ (- 1)) \ cdot A = E $, zatem macierze $ ((A) ^ (- 1)) $ i $ A $ są również dopasowane we wskazanej kolejności:

\ [\ begin (align) & \ left [a \ razy b \ w prawo] \ cdot \ w lewo [m \ razy n \ w prawo] = \ w lewo [a \ razy n \ w prawo] \\ & b = m \ koniec ( wyrównywać) \]

Zatem bez utraty ogólności możemy założyć, że $ A = \ lewo [m \ razy n \ prawo] $, $ ((A) ^ (- 1)) = \ lewo [n \ razy m \ prawo] $. Jednak zgodnie z definicją $ A \ cdot ((A) ^ (- 1)) = ((A) ^ (- 1)) \ cdot A $, więc rozmiary macierzy są dokładnie takie same:

\ [\ początek (wyrównaj) & \ lewo [m \ razy n \ prawo] = \ lewo [n \ razy m \ prawo] \\ & m = n \ koniec (wyrównaj) \]

Okazuje się więc, że wszystkie trzy macierze - $ A $, $ ((A) ^ (- 1)) $ i $ E $ - to rozmiary kwadratowe $ \ lewo [n \ razy n \ prawo] $. Lemat jest udowodniony.

Cóż, to już nie jest złe. Widzimy, że tylko macierze kwadratowe są odwracalne. Teraz upewnijmy się, że odwrotność jest zawsze taka sama.

Lemat 2. Mając macierz $ A $ i jej odwrotność $ ((A) ^ (- 1)) $. Wtedy ta odwrotność jest jedyna.

Dowód. Idźmy odwrotnie: niech macierz $ A $ ma co najmniej dwie kopie swojej odwrotności - $ B $ i $ C $. Wówczas zgodnie z definicją prawdziwe są następujące równości:

\ [\ rozpocznij (wyrównaj) & A \ cdot B = B \ cdot A = E; \\ & A \ cdot C = C \ cdot A = E. \\ \ koniec (wyrównaj) \]

Z Lematu 1 wnioskujemy, że wszystkie cztery macierze - $ A $, $ B $, $ C $ i $ E $ - są kwadratami tej samej kolejności: $ \ lewo [n \ razy n \ prawo] $. Dlatego produkt jest zdefiniowany:

Ponieważ mnożenie macierzy jest asocjacyjne (ale nie przemienne!), możemy napisać:

\ [\ begin (wyrównaj) & B \ cdot A \ cdot C = \ left (B \ cdot A \ right) \ cdot C = E \ cdot C = C; \\ & B \ cdot A \ cdot C = B \ cdot \ left (A \ cdot C \ right) = B \ cdot E = B; \\ & B \ cdot A \ cdot C = C = B \ Strzałka w prawo B = C. \\ \ koniec (wyrównaj) \]

Otrzymał jedyną rzecz możliwy wariant: dwa wystąpienia macierzy odwrotnej są równe. Lemat jest udowodniony.

Powyższe rozumowanie powtarza niemal słowo w słowo dowód na niepowtarzalność odwrotności dla wszystkich liczb rzeczywistych $ b \ ne 0 $. Jedynym niezbędnym dodatkiem jest uwzględnienie wymiaru matryc.

Jednak nadal nie wiemy nic o tym, czy jakakolwiek macierz kwadratowa jest odwracalna. Tu z pomocą przychodzi nam wyznacznik – to kluczowa cecha wszystkich macierzy kwadratowych.

Lemat 3. Dostajesz macierz $ A $. Jeśli istnieje jej macierz odwrotna $ ((A) ^ (- 1)) $, to wyznacznik pierwotnej macierzy jest niezerowy:

\ [\ lewo | A \ prawo | \ ne 0 \]

Dowód. Wiemy już, że $ A $ i $ ((A) ^ (- 1)) $ to macierze kwadratowe o rozmiarze $ \ left [n \ razy n \ right] $. Dlatego dla każdego z nich można obliczyć wyznacznik: $ \ left | A \ prawo | $ i $ \ lewo | ((A) ^ (- 1)) \ prawo | $. Jednak wyznacznik iloczynu jest równy iloczynowi wyznaczników:

\ [\ lewo | A \ cdot B \ prawo | = \ lewo | A \ prawo | \ cdot \ lewo | B \ prawo | \ Prawostrzałka \ lewo | A \ cdot ((A) ^ (- 1)) \ prawo | = \ lewo | A \ prawo | \ cdot \ lewo | ((A) ^ (- 1)) \ prawo | \]

Ale zgodnie z definicją $ A \ cdot ((A) ^ (- 1)) = E $, a wyznacznikiem $ E $ jest zawsze 1, zatem

\ [\ rozpocznij (wyrównaj) & A \ cdot ((A) ^ (- 1)) = E; \\ & \ lewo | A \ cdot ((A) ^ (- 1)) \ prawo | = \ lewo | E \ prawo |; \\ & \ lewo | A \ prawo | \ cdot \ lewo | ((A) ^ (- 1)) \ prawo | = 1. \\ \ koniec (wyrównaj) \]

Iloczyn dwóch liczb jest równy jeden tylko wtedy, gdy każda z tych liczb jest różna od zera:

\ [\ lewo | A \ right | \ ne 0; \ quad \ left | ((A) ^ (- 1)) \ prawo | \ ne 0. \]

Okazuje się więc, że $ \ left | \ prawo | \ ne 0 $. Lemat jest udowodniony.

W rzeczywistości ten wymóg jest dość logiczny. Teraz przeanalizujemy algorytm znajdowania macierzy odwrotnej - i stanie się całkiem jasne, dlaczego przy zerowym wyznaczniku w zasadzie nie może istnieć żadna macierz odwrotna.

Ale najpierw sformułujmy „pomocniczą” definicję:

Definicja. Macierz zdegenerowana to macierz kwadratowa o rozmiarze $ \ lewo [n \ razy n \ prawo] $, której wyznacznikiem jest zero.

W ten sposób możemy stwierdzić, że każda macierz odwracalna jest niezdegenerowana.

Jak znaleźć odwrotność macierzy

Teraz rozważymy uniwersalny algorytm znajdowania macierzy odwrotnych. Ogólnie rzecz biorąc, istnieją dwa ogólnie przyjęte algorytmy, a dziś również rozważymy drugi.

Ta, która zostanie teraz omówiona, jest bardzo wydajna dla macierzy o rozmiarze $ \ left [2 \ razy 2 \ right] $ i - częściowo - o rozmiarze $ \ left [3 \ razy 3 \ right] $. Ale zaczynając od rozmiaru $ \ lewo [4 \ razy 4 \ prawo] $ lepiej go nie używać. Dlaczego - teraz sam wszystko zrozumiesz.

Uzupełnienia algebraiczne

Przygotuj się. Teraz będzie ból. Nie, nie martw się: piękna pielęgniarka w spódnicy, pończochach ze sznurowadłami i nie zrobi ci zastrzyku w pośladek. Wszystko jest o wiele bardziej prozaiczne: nadchodzą do was dodatki algebraiczne i Jej Królewska Mość „Union Matrix”.

Zacznijmy od najważniejszej rzeczy. Niech będzie macierz kwadratowa o rozmiarze $ A = \ left [n \ razy n \ right] $, której elementy nazywają się $ ((a) _ (ij)) $. Następnie dla każdego takiego elementu można zdefiniować dopełnienie algebraiczne:

Definicja. Uzupełnienie algebraiczne $ ((A) _ (ij)) $ do elementu $ ((a) _ (ij)) $ znajdującego się w $ i $ -tym wierszu i $ j $ -tej kolumnie macierzy $ A = \ left [n \ razy n \ prawo] $ jest konstrukcją postaci

\ [((A) _ (ij)) = ((\ lewo (-1 \ prawo)) ^ (i + j)) \ cdot M_ (ij) ^ (*) \]

Gdzie $ M_ (ij) ^ (*) $ jest wyznacznikiem macierzy otrzymanej z oryginalnego $ A $ przez usunięcie tego samego $ i $ -tego wiersza i $ j $ -tej kolumny.

Jeszcze raz. Uzupełnienie algebraiczne do elementu macierzy o współrzędnych $ \ left (i; j \ right) $ oznaczamy jako $ ((A) _ (ij)) $ i oblicza się według schematu:

Najpierw usuń wiersz $ i $ - oraz kolumnę $ j $ -th z oryginalnej macierzy. Otrzymujemy nową macierz kwadratową i oznaczamy jej wyznacznik jako $ M_ (ij) ^ (*) $.
Następnie mnożymy ten wyznacznik przez $ ((\ left (-1 \ right)) ^ (i + j)) $ - na pierwszy rzut oka to wyrażenie może wydawać się nudne, ale w rzeczywistości dopiero odkrywamy znak przed $ M_ (ij) ^ (*) $.
Liczymy - otrzymujemy konkretną liczbę. Tych. uzupełnienie algebraiczne jest dokładnie liczbą, a nie jakąś nową macierzą itp.

Sama macierz $ M_ (ij) ^ (*) $ jest nazywana komplementarną podrzędną do elementu $ ((a) _ (ij)) $. I w tym sensie powyższa definicja dopełnienia algebraicznego jest szczególnym przypadkiem definicji bardziej złożonej - co rozważaliśmy w lekcji o wyznaczniku.

Ważna uwaga. Ogólnie rzecz biorąc, w matematyce „dorosłych” dodatki algebraiczne definiuje się w następujący sposób:

Bierzemy $k $ wiersze i $k $ kolumny w macierzy kwadratowej. Na ich przecięciu otrzymujemy macierz o rozmiarze $ \ left [k \ razy k \ right] $ - jej wyznacznik nazywamy minorem rzędu $ k $ i jest oznaczony przez $ ((M) _ (k)) $.

Następnie usuwamy te „ulubione” wiersze $k $ i kolumny $k $. Znowu otrzymujemy macierz kwadratową - jej wyznacznik nazywamy komplementarną podrzędną i oznaczamy $ M_ (k) ^ (*) $.

Pomnóż $ M_ (k) ^ (*) $ przez $ ((\ left (-1 \ right)) ^ (t)) $, gdzie $ t $ to (teraz uwaga!) Suma liczb wszystkich zaznaczonych linii i kolumny ... To będzie dodatek algebraiczny.

Spójrz na trzeci krok: w rzeczywistości jest suma warunków $ 2k $! Inna sprawa, że dla $ k = 1 $ otrzymamy tylko 2 wyrazy - będą to te same $ i + j $ - "współrzędne" elementu $ ((a) _ (ij)) $, którego szukamy dla uzupełnienia algebraicznego.

Dlatego dzisiaj posługujemy się nieco uproszczoną definicją. Ale jak zobaczymy później, to będzie więcej niż wystarczające. Kolejna rzecz jest o wiele ważniejsza:

Definicja. Macierz sprzężona $ S $ do macierzy kwadratowej $ A = \ left [n \ razy n \ right] $ jest nową macierzą o rozmiarze $ \ left [n \ razy n \ right] $, którą otrzymuje się z $ A $ zastępując $ ((a) _ (ij)) $ uzupełnienia algebraiczne $ ((A) _ (ij)) $:

\\ Strzałka w prawo S = \ lewo [\ początek (macierz) ((A) _ (11)) & ((A) _ (12)) & ... & ((A) _ (1n)) \\ (( A) _ (21)) & ((A) _ (22)) & ... & ((A) _ (2n)) \\ ... & ... & ... & ... \\ ((A) _ (n1)) & ((A) _ (n2)) & ... & ((A) _ (nn)) \\\ end (macierz) \ prawo] \]

Pierwsza myśl, jaka nasuwa się w momencie realizacji tej definicji to „tyle trzeba liczyć!” Spokojnie: będziesz musiał liczyć, ale nie tak bardzo :)

Cóż, to wszystko jest bardzo miłe, ale dlaczego jest to konieczne? Dlatego.

Główne twierdzenie

Cofnijmy się trochę. Pamiętaj, w Lemie 3 stwierdzono, że macierz odwracalna $ A $ jest zawsze niezdegenerowana (czyli jej wyznacznik jest niezerowy: $ \ left | A \ right | \ ne 0 $).

Tak więc jest też odwrotnie: jeśli macierz $ A $ nie jest zdegenerowana, to zawsze jest odwracalna. I jest nawet schemat wyszukiwania $ ((A) ^ (- 1)) $. Sprawdź to:

Twierdzenie o macierzy odwrotnej. Niech będzie dana macierz kwadratowa $ A = \ left [n \ razy n \ right] $, której wyznacznik jest niezerowy: $ \ left | \ prawo | \ ne 0 $. Wtedy macierz odwrotna $ ((A) ^ (- 1)) $ istnieje i jest obliczana według wzoru:

\ [((A) ^ (- 1)) = \ frac (1) (\ lewo | A \ prawo |) \ cdot ((S) ^ (T)) \]

A teraz – wszystko jest takie samo, ale czytelnym pismem. Aby znaleźć odwrotność macierzy, potrzebujesz:

Oblicz wyznacznik $ \ left | \ right | $ i upewnij się, że jest niezerowe.
Skonstruuj macierz sumy $ S $, tj. policz 100500 uzupełnień algebraicznych $ ((A) _ (ij)) $ i umieść je w miejscu $ ((a) _ (ij)) $.
Transponuj tę macierz $ S $, a następnie pomnóż ją przez jakąś liczbę $ q = (1) / (\ left | A \ right |) \; $.

I to wszystko! Znaleziono macierz odwrotną $ ((A) ^ (- 1)) $. Rzućmy okiem na przykłady:

\ [\ lewo [\ początek (macierz) 3 i 1 \\ 5 i 2 \\\ koniec (macierz) \ prawo] \]

Rozwiązanie. Sprawdźmy odwracalność. Obliczmy wyznacznik:

\ [\ lewo | A \ prawo | = \ lewo | \ begin (macierz) 3 & 1 \\ 5 & 2 \\\ end (macierz) \ right | = 3 \ cdot 2-1 \ cdot 5 = 6-5 = 1 \]

Wyznacznik jest niezerowy. Stąd macierz jest odwracalna. Skomponujmy macierz unii:

Policzmy dodatki algebraiczne:

\ [\ begin (align) & ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | 2 \ prawo |= 2; \\ & ((A) _ (12)) = ((\ lewo (-1 \ prawo)) ^ (1 + 2)) \ cdot \ lewo | 5 \ prawo | = -5; \\ & ((A) _ (21)) = ((\ lewo (-1 \ prawo)) ^ (2 + 1)) \ cdot \ lewo | 1 \ prawo | = -1; \\ & ((A) _ (22)) = ((\ lewo (-1 \ prawo)) ^ (2 + 2)) \ cdot \ lewo | 3 \ w prawo | = 3. \\ \ koniec (wyrównaj) \]

Uwaga: wyznaczniki | 2 |, | 5 |, | 1 | oraz |3 | - są to wyznaczniki macierzy o rozmiarze $ \ left [1 \ razy 1 \ right] $, a nie moduły. Tych. jeśli uwzględniono kwalifikatory liczby ujemne, nie jest konieczne usuwanie „minusu”.

W sumie nasza macierz unii wygląda tak:

\ [((A) ^ (- 1)) = \ frac (1) (\ lewa | A \ prawa |) \ cdot ((S) ^ (T)) = \ frac (1) (1) \ cdot ( (\ left [\ begin (array) (* (35) (r)) 2 & -5 \\ -1 & 3 \\\ end (array) \ right]) ^ (T)) = \ left [\ begin (tablica) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (tablica) \ prawo] \]

OK, już po wszystkim. Problem został rozwiązany.

Odpowiedź. $ \ left [\ begin (tablica) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (tablica) \ right] $

Zadanie. Znajdź odwrotność macierzy:

\ [\ left [\ begin (tablica) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (tablica) \ right] \]

Rozwiązanie. Ponownie rozważamy wyznacznik:

\ [\ początek (wyrównaj) & \ lewo | \ begin (tablica) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (tablica) \ right | = \ begin (macierz ) \ lewo (1 \ cdot 2 \ cdot 1+ \ lewo (-1 \ prawo) \ cdot \ lewo (-1 \ prawo) \ cdot 1 + 2 \ cdot 0 \ cdot 0 \ prawo) - \\ - \ lewo (2 \ cdot 2 \ cdot 1+ \ lewy (-1 \ prawy) \ cdot 0 \ cdot 1 + 1 \ cdot \ lewy (-1 \ prawy) \ cdot 0 \ prawy) \\\ end (matryca) = \ \ & = \ lewo (2 + 1 + 0 \ prawo) - \ lewo (4 + 0 + 0 \ prawo) = - 1 \ ne 0. \\ \ end (wyrównaj) \]

Wyznacznik jest niezerowy - macierz jest odwracalna. Ale teraz będzie najtrudniejszy: trzeba policzyć aż 9 (dziewięć, cholera!) Dodatków algebraicznych. I każdy z nich będzie zawierał kwalifikator $ \ lewo [2 \ razy 2 \ prawo] $. Latał:

\ [\ begin (macierz) ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (macierz) 2 & -1 \\ 0 & 1 \\\ end (macierz) \ right |= 2; \\ ((A) _ (12)) = ((\ lewo (-1 \ prawo)) ^ (1 + 2)) \ cdot \ lewo | \ początek (macierz) 0 & -1 \\ 1 & 1 \\\ koniec (macierz) \ prawo | = -1; \\ ((A) _ (13)) = ((\ lewo (-1 \ prawo)) ^ (1 + 3)) \ cdot \ lewo | \ początek (macierz) 0 & 2 \\ 1 & 0 \\\ koniec (macierz) \ prawo | = -2; \\ ... \\ ((A) _ (33)) = ((\ lewo (-1 \ prawo)) ^ (3 + 3)) \ cdot \ lewo | \ begin (macierz) 1 & -1 \\ 0 & 2 \\\ end (macierz) \ right |= 2; \\ \ koniec (matryca) \]

Krótko mówiąc, macierz unii będzie wyglądać tak:

Dlatego odwrotność macierzy będzie wyglądać tak:

\ [((A) ^ (- 1)) = \ frac (1) (- 1) \ cdot \ left [\ początek (macierz) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\ end (macierz) \ right] = \ left [\ begin (tablica) (* (35) (r)) - 2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\ koniec (tablica) \ prawo] \]

Cóż, to wszystko. Oto odpowiedź.

Odpowiedź. $ \ left [\ begin (tablica) (* (35) (r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\ end (tablica) \ right ] $

Jak widać, na końcu każdego przykładu przeprowadziliśmy kontrolę. W związku z tym ważna uwaga:

Nie bądź leniwy, aby sprawdzić. Pomnóż oryginalną macierz przez znalezioną odwrotność - powinieneś otrzymać $ E $.

To sprawdzenie jest znacznie łatwiejsze i szybsze niż szukanie błędu w dalszych obliczeniach, gdy np. rozwiązujesz równanie macierzowe.

Alternatywny sposób

Jak powiedziałem, twierdzenie o macierzy odwrotnej działa świetnie dla rozmiarów $ \ left [2 \ times 2 \ right] $ i $ \ left [3 \ times 3 \ right] $ (w ten drugi przypadek- nie jest tak "świetnie"), ale dla dużych matryc zaczyna się smutek.

Ale nie martw się: istnieje alternatywny algorytm, za pomocą którego można spokojnie znaleźć odwrotność nawet dla macierzy $ \ lewo [10 \ razy 10 \ prawo] $. Ale, jak to często bywa, aby rozważyć ten algorytm, potrzebujemy trochę podstaw teoretycznych.

Przekształcenia elementarne

Wśród różnych przekształceń macierzy jest kilka specjalnych - nazywane są one elementarnymi. Są dokładnie trzy takie przekształcenia:

Mnożenie. Możesz wziąć wiersz (kolumnę) $ i $ i pomnożyć go przez dowolną liczbę $ k \ ne 0 $;
Dodatek. Dodaj do $ i $ th wiersz (kolumnę) dowolny inny $ j $ th wiersz (kolumnę) pomnożony przez dowolną liczbę $ k \ ne 0 $ (możesz, oczywiście, i $ k = 0 $, ale po co? Nic się jednak nie zmieni).
Przegrupowanie. Weź wiersze (kolumny) $ i $ th oraz $ j $ th i zamień je.

Dlaczego te przekształcenia nazywamy elementarnymi (dla dużych matryc nie wyglądają tak elementarnie) i dlaczego są ich tylko trzy – te pytania wykraczają poza zakres dzisiejszej lekcji. Dlatego nie będziemy wchodzić w szczegóły.

Inna sprawa jest ważna: wszystkie te perwersje musimy wykonać na załączonej matrycy. Tak, tak: dobrze słyszałeś. Teraz będzie jeszcze jedna definicja - ostatnia w dzisiejszej lekcji.

Dołączona matryca

Na pewno w szkole rozwiązywałeś układy równań metodą dodawania. Cóż, odejmij inny od jednego ciągu, pomnóż jakiś ciąg przez liczbę - to wszystko.

A więc: teraz wszystko będzie takie samo, ale już „w dorosły sposób”. Gotowe?

Definicja. Niech zostanie podana macierz $ A = \ lewo [n \ razy n \ prawo] $ oraz macierz jednostkowa $ E $ o tym samym rozmiarze $ n $. Wtedy macierz sprzężona $ \ left [A \ left | E \ prawo. \ right] $ to nowa macierz $ \ left [n \ razy 2n \ right] $, która wygląda tak:

\ [\ lewo [A \ lewo | E \ prawo. \ right] = \ left [\ begin (array) (rrrr | rrrr) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) & 1 & 0 & ... & 0 \\ ((a) _ (21)) & ((a) _ (22)) & ... & ((a) _ (2n)) & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... \\ ((a) _ (n1)) & ((a) _ (n2)) & ... & ((a) _ (nn)) & 0 & 0 & ... & 1 \\\ koniec (tablica) \ prawo] \]

W skrócie bierzemy macierz $A $, po prawej stronie przypisujemy do niej macierz tożsamości $E $ o wymaganej wielkości, oddzielamy je pionową kreską dla piękna - oto dołączona :)

Jaki jest haczyk? Oto co:

Twierdzenie. Niech macierz $ A $ będzie odwracalna. Rozważmy macierz sprzężoną $ \ left [A \ left | E \ prawo. \ prawo] $. Jeśli używasz podstawowe konwersje ciągów doprowadź do postaci $ \ left [E \ left | Jasny. \ prawo] $, czyli mnożąc, odejmując i przestawiając wiersze, aby uzyskać z $ A $ macierz $ E $ po prawej stronie, to macierz $ B $ otrzymana po lewej stronie jest odwrotnością $ A $:

\ [\ lewo [A \ lewo | E \ prawo. \ prawo] \ do \ lewo [E \ lewo | Jasny. \ prawo] \ Strzałka w prawo B = ((A) ^ (- 1)) \]

To takie proste! W skrócie algorytm znajdowania macierzy odwrotnej wygląda tak:

Napisz dołączoną macierz $ \ left [A \ left | E \ prawo. \ prawo] $;
Wykonuj podstawowe konwersje łańcuchów, aż pojawi się $ E $ zamiast $ A $;
Oczywiście po lewej też coś pojawi się - jakaś matryca $B$. To będzie odwrotnie;
ZYSK!:)

Oczywiście łatwiej to powiedzieć niż zrobić. Spójrzmy więc na kilka przykładów: dla rozmiarów $ \ lewy [3 \ razy 3 \ prawy] $ i $ \ lewy [4 \ razy 4 \ prawy] $.

Zadanie. Znajdź odwrotność macierzy:

\ [\ lewo [\ początek (tablica) (* (35) (r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\ koniec (tablica) \ prawo] \ ]

Rozwiązanie. Komponujemy załączoną matrycę:

\ [\ lewo [\ początek (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 i 1 \\\ koniec (tablica) \ prawo] \]

Ponieważ ostatnia kolumna oryginalnej macierzy jest wypełniona jedynkami, odejmijmy pierwszy wiersz od reszty:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\ end (tablica) \ prawo] \ begin (macierz) \ downarrow \\ -1 \\ -1 \\\ end (macierz) \ do \\ & \ do \ lewo [\ początek (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ koniec (tablica) \ prawo] \\ \ koniec (wyrównaj) \]

Nie ma więcej, z wyjątkiem pierwszej linii. Ale nie dotykamy tego, w przeciwnym razie w trzeciej kolumnie nowo usunięte jednostki zaczną się „mnożyć”.

Ale możemy odjąć drugą linię dwa razy od ostatniej - otrzymujemy ją w lewym dolnym rogu:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end (tablica) \ prawo] \ begin (macierz) \ \\ \ downarrow \\ -2 \\\ end (macierz) \ to \\ & \ left [\ początek (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ koniec (tablica) \ prawo] \\ \ koniec (wyrównaj) \]

Teraz możemy odjąć ostatni wiersz od pierwszego i dwukrotnie od drugiego - w ten sposób "zerujemy" pierwszą kolumnę:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (tablica) \ right] \ begin (macierz) -1 \\ -2 \\ \ uparrow \\\ end (macierz) \ to \\ & \ do \ lewo [\ początek (tablica) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ koniec (tablica) \ prawo] \\ \ koniec (wyrównaj) \]

Pomnóż drugi rząd przez -1, a następnie odejmij go 6 razy od pierwszego i dodaj 1 raz do ostatniego:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (tablica) \ right] \ begin (macierz) \ \\ \ left | \ cdot \ lewy (-1 \ prawy) \ prawy. \\ \\\ end (matryca) \ to \\ & \ to \ left [\ begin (tablica) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (tablica) \ right] \ begin (macierz) -6 \\ \ updownarrow \\ +1 \\\ end ( macierz) \ do \\ & \ do \ lewo [\ początek (tablica) (rrr | rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \ \ 1 & 0 & 0 & 4 & -7 & 3 \\\ end (tablica) \ right] \\ \ end (align) \]

Pozostaje tylko zamienić linie 1 i 3:

\ [\ lewo [\ początek (tablica) (rrr | rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 i 32 i -13 \\\ koniec (tablica) \ prawo] \]

Gotowe! Po prawej stronie znajduje się pożądana macierz odwrotna.

Odpowiedź. $ \ left [\ begin (tablica) (* (35) (r)) 4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\ end (tablica) \ right ] $

Zadanie. Znajdź odwrotność macierzy:

\ [\ lewo [\ początek (matryca) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\ koniec (matryca) \ prawy] \]

Rozwiązanie. Ponownie tworzymy załączony:

\ [\ lewo [\ początek (tablica) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 i -1 i 1 i 1 i 0 i 0 i 1 i 0 \\ 0 i -10 i -2 i -5 i 0 i 0 i 0 i 1 \\\ koniec (tablica) \ prawo] \]

Bądźmy trochę śpiący, żałujmy, ile musimy teraz liczyć ... i zacznijmy liczyć. Najpierw wyzerujmy pierwszą kolumnę, odejmując wiersz 1 od wierszy 2 i 3:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 i 0 i 0 \\ 1 i -1 i 1 i 1 i 0 i 0 i 1 i 0 \\ 0 i -10 i -2 i -5 i 0 i 0 i 0 i 1 \\\ koniec (tablica) \ right] \ begin (macierz) \ downarrow \\ -1 \\ -1 \\ \\\ end (macierz) \ to \\ & \ to \ left [\ begin (tablica) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (tablica) \ prawo] \\ \ end (wyrównaj) \]

Widzimy zbyt wiele „przeciw” w wierszach 2-4. Pomnóż wszystkie trzy wiersze przez -1, a następnie wypal trzecią kolumnę, odejmując wiersz 3 od reszty:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 i 1 i 0 i 0 \\ 0 i -5 i -1 i -2 i -1 i 0 i 1 i 0 \\ 0 i -10 i -2 i -5 i 0 i 0 i 0 i 1 \\ \ end (tablica) \ right] \ begin (macierz) \ \\ \ left | \ cdot \ lewy (-1 \ prawy) \ prawy. \\ \ lewo | \ cdot \ lewy (-1 \ prawy) \ prawy. \\ \ lewo | \ cdot \ lewy (-1 \ prawy) \ prawy. \\\ end (matryca) \ to \\ & \ to \ left [\ begin (tablica) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 i 1 i -1 i 0 i 0 \\ 0 i 5 i 1 i 2 i 1 i 0 i -1 i 0 \\ 0 i 10 i 2 i 5 i 0 i 0 i 0 i -1 \\ \ end (tablica) \ right] \ begin (macierz) -2 \\ -1 \\ \ updownarrow \\ -2 \\\ end (macierz) \ to \\ & \ to \ left [\ begin (tablica) ( rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (tablica) \ prawo] \\ \ end (wyrównaj) \]

Teraz nadszedł czas, aby „usmażyć” ostatnią kolumnę oryginalnej macierzy: odejmij wiersz 4 od reszty:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ koniec (tablica ) \ right] \ begin (macierz) +1 \\ -3 \\ -2 \\ \ uparrow \\\ end (macierz) \ to \\ & \ to \ left [\ begin (tablica) (rrrr | rrrr) 1 i -6 i 0 i 0 i -3 i 0 i 4 i -1 \\ 0 i 1 i 0 i 0 i 6 i -1 i -5 i 3 \\ 0 i 5 i 1 i 0 i 5 i 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (tablica) \ prawo] \\ \ end (wyrównaj) \]

Rzut końcowy: Wypal drugą kolumnę, odejmując wiersz 2 od wierszy 1 i 3:

\ [\ begin (wyrównaj) & \ left [\ begin (tablica) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 i -1 i -5 i 3 \\ 0 i 5 i 1 i 0 i 5 i 0 i -5 i 2 \\ 0 i 0 i 0 i 1 i -2 i 0 i 2 i -1 \\\ koniec ( array) \ right] \ begin (matrix) 6 \\ \ updownarrow \\ -5 \\ \ \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 i 0 i 0 i 0 i 33 i -6 i -26 i -17 \\ 0 i 1 i 0 i 0 i 6 i -1 i -5 i 3 \\ 0 i 0 i 1 i 0 i -25 i 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (tablica) \ right] \\ \ end (align) \]

I znowu po lewej stronie jest macierz jednostkowa, co oznacza, że po prawej stronie jest odwrotność :)

Odpowiedź. $ \ lewo [\ początek (matryca) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\ koniec (matryca) \ prawo] $

OK, już po wszystkim. Sprawdź sam - złom dla mnie :)

W tym artykule omówimy macierzową metodę rozwiązywania układu liniowych równań algebraicznych, znajdziemy jej definicję i podamy przykłady rozwiązania.

Definicja 1

Metoda macierzy odwrotnej to metoda używana do rozwiązywania SLAE w przypadku, gdy liczba niewiadomych jest równa liczbie równań.

Przykład 1

Znajdź rozwiązanie układu n równań liniowych z n niewiadomymi:

11 x 1 + 12 x 2 +. ... ... + a 1 n x n = b 1 za n 1 x 1 + za n 2 x 2 +. ... ... + a n n x n = b n

Typ zapisu matrycowego : A × X = B

gdzie A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 an 2 ⋯ a n n jest macierzą układu.

X = x 1 x 2 ⋮ x n - kolumna niewiadomych,

B = b 1 b 2 ⋮ b n - kolumna wolnych współczynników.

Z równania, które otrzymaliśmy, musisz wyrazić X. Aby to zrobić, musisz pomnożyć obie strony równania macierzowego po lewej stronie przez A - 1:

A - 1 × A × X = A - 1 × B.

Ponieważ A - 1 × A = E, to E × X = A - 1 × B lub X = A - 1 × B.

Komentarz

Macierz odwrotna do macierzy A ma prawo istnieć tylko wtedy, gdy warunek d e t A nie jest równy zero. Dlatego przy rozwiązywaniu SLAE metodą macierzy odwrotnej przede wszystkim d e t A.

Jeżeli d e t A nie jest równe zero, system ma tylko jedno rozwiązanie: zastosowanie metody macierzy odwrotnej. Jeśli d e t А = 0, to układ nie może być rozwiązany tą metodą.

Przykład rozwiązania układu równań liniowych metodą macierzy odwrotnej

Przykład 2

SLAE rozwiązujemy metodą macierzy odwrotnej:

2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2

Jak rozwiązać?

Układ zapisujemy w postaci równania macierzowego A X = B, gdzie

A = 2 - 4 3 1 - 2 4 3 - 1 5, X = x 1 x 2 x 3, B = 1 3 2.

Wyrażamy z tego równania X:

Znajdź wyznacznik macierzy A:

det A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25

d e t А nie jest równe 0, dlatego metoda rozwiązania macierzy odwrotnej jest odpowiednia dla tego układu.

Znajdź macierz odwrotną A - 1 za pomocą macierzy sumy. Obliczamy uzupełnienia algebraiczne A i j do odpowiednich elementów macierzy A:

A 11 = (- 1) (1 + 1) - 2 4 - 1 5 = - 10 + 4 = - 6,

A 12 = (- 1) 1 + 2 1 4 3 5 = - (5 - 12) = 7,

A 13 = (- 1) 1 + 3 1 - 2 3 - 1 = - 1 + 6 = 5,

A 21 = (- 1) 2 + 1 - 4 3 - 1 5 = - (- 20 + 3) = 17,

A 22 = (- 1) 2 + 2 2 3 3 5 - 10 - 9 = 1,

A 23 = (- 1) 2 + 3 2 - 4 3 - 1 = - (- 2 + 12) = - 10,

A 31 = (- 1) 3 + 1 - 4 3 - 2 4 = - 16 + 6 = - 10,

A 32 = (- 1) 3 + 2 2 3 1 4 = - (8 - 3) = - 5,

A 33 = (- 1) 3 + 3 2 - 4 1 - 2 = - 4 + 4 = 0.

Zapisujemy macierz sumy A *, która składa się z algebraicznych dopełnień macierzy A:

A * = - 6 7 5 17 1 - 10 - 10 - 5 0

Macierz odwrotną zapisujemy według wzoru:

A - 1 = 1 d e t A (A *) T: A - 1 = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

Mnożymy macierz odwrotną A - 1 przez kolumnę wyrazów wolnych B i otrzymujemy rozwiązanie układu:

X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1

Odpowiedź : x 1 = - 1; x 2 = 0; x 3 = 1

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl + Enter