Curso de mecánica teórica de conferencias. Curso de conferencias mecánica técnica

1 diapositiva

Curso de conferencias sobre mecánica teórica Dinámica (parte I) Bondarenko A.N. Moscú - 2007 El curso de capacitación electrónico se escribió sobre la base de conferencias impartidas por el autor para estudiantes que estudian las especialidades de SZhD, PGS y SDM en NIIZhT y MIIT (1974-2006). Material educativo corresponde planes de calendario durante tres semestres. Para implementar completamente los efectos de animación durante una presentación, debe usar un visor de Power Point no inferior al de Microsoft Office incorporado. Sistema operativo Windows-XP Profesional. Los comentarios y sugerencias pueden enviarse por correo electrónico: [correo electrónico protegido]. Universidad Estatal de Ingeniería Ferroviaria de Moscú (MIIT) Departamento de Mecánica Teórica Centro Científico y Técnico de Tecnologías de Transporte

2 diapositivas

Contenidos Tema 1. Introducción a la dinámica. Leyes y axiomas de la dinámica punto material. Ecuación básica de la dinámica. Ecuaciones de movimiento diferenciales y naturales. Dos tareas principales de la dinámica. Ejemplos de resolución del problema directo de la dinámica Tema 2. Resolución del problema inverso de la dinámica. Instrucciones generales a la solución del problema inverso de la dinámica. Ejemplos de resolución del problema inverso de la dinámica. El movimiento de un cuerpo lanzado en ángulo con respecto al horizonte, sin tener en cuenta la resistencia del aire. Tema 3. Oscilaciones rectilíneas de un punto material. La condición para la ocurrencia de oscilaciones. Clasificación de las vibraciones. Vibraciones libres sin tener en cuenta las fuerzas de resistencia. vibraciones amortiguadas. Decremento de oscilación. Tema 4. Oscilaciones forzadas de un punto material. Resonancia. Influencia de la resistencia al movimiento durante vibraciones forzadas. Tema 5. Movimiento relativo de un punto material. Fuerzas de inercia. Casos particulares de movimiento para varios tipos de movimiento portátil. Influencia de la rotación de la Tierra en el equilibrio y movimiento de los cuerpos. Tema 6. Dinámica de un sistema mecánico. sistema mecánico. Fuerzas externas e internas. Centro de masa del sistema. El teorema del movimiento del centro de masa. Leyes de conservación. Un ejemplo de cómo resolver el problema de usar el teorema sobre el movimiento del centro de masa. Tema 7. Impulso de fuerza. La cantidad de movimiento. Teorema del cambio de cantidad de movimiento. Leyes de conservación. el teorema de Euler. Un ejemplo de resolución del problema sobre el uso del teorema sobre el cambio en el momento. momento de impulso. El teorema de la variación del momento angular Tema 8. Leyes de conservación. Elementos de la teoría de los momentos de inercia. Momento cinético de un cuerpo rígido. Ecuación diferencial Rotación de un cuerpo rígido. Un ejemplo de cómo resolver el problema de usar el teorema para cambiar el momento angular del sistema. Teoría elemental del giroscopio. Literatura recomendada 1. Yablonsky A.A. Curso de mecánica teórica. Parte 2. METRO.: escuela secundaria. 1977. 368 págs. 2. Meshchersky I.V. Colección de problemas de mecánica teórica. M.: Ciencia. 1986 416 págs. 3. Colección de tareas para Papeles de termino/ Ed. AUTOMÓVIL CLUB BRITÁNICO. Yablonsky. M.: Escuela superior. 1985. 366 págs. 4. Bondarenko A. N. “ Mecánica teórica en ejemplos y tareas. Dynamics” (manual electrónico www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 diapositivas

Clase 1 Dinámica es una sección de mecánica teórica que estudia el movimiento mecánico desde el principio. punto común visión. El movimiento se considera en relación con las fuerzas que actúan sobre el objeto. La sección consta de tres secciones: Dinámica de un punto material Dinámica Dinámica de un sistema mecánico Mecánica analítica ■ Dinámica de un punto - estudia el movimiento de un punto material, teniendo en cuenta las fuerzas que provocan este movimiento. El objeto principal es un punto material: un cuerpo material con una masa, cuyas dimensiones pueden despreciarse. Supuestos básicos: - existe un espacio absoluto (tiene propiedades puramente geométricas que no dependen de la materia y su movimiento). - existe un tiempo absoluto (no depende de la materia y su movimiento). Se sigue de esto: - existe un marco de referencia absolutamente inmóvil - el tiempo no depende del movimiento del marco de referencia - las masas de los puntos en movimiento no dependen del movimiento del marco de referencia Estas suposiciones se utilizan en la mecánica clásica creada por Galileo y Newton Todavía tiene un alcance bastante amplio, ya que los sistemas mecánicos considerados en ciencias aplicadas no tienen tal en numeros grandes y velocidades de movimiento, para lo cual es necesario tener en cuenta su influencia en la geometría del espacio, el tiempo, el movimiento, como se hace en la mecánica relativista (la teoría de la relatividad). ■ Las leyes básicas de la dinámica, descubiertas por primera vez por Galileo y formuladas por Newton, forman la base de todos los métodos para describir y analizar el movimiento de los sistemas mecánicos y su interacción dinámica bajo la acción de varias fuerzas. ■ Ley de inercia (ley de Galileo-Newton) - Un punto material aislado de un cuerpo conserva su estado de reposo o uniforme movimiento rectilíneo hasta que las fuerzas aplicadas hacen que cambie ese estado. Esto implica la equivalencia del estado de reposo y movimiento por inercia (la ley de la relatividad de Galileo). El marco de referencia, en relación con el cual se cumple la ley de la inercia, se denomina inercial. La propiedad de un punto material de esforzarse por mantener invariable la velocidad de su movimiento (su estado cinemático) se llama inercia. ■ La ley de proporcionalidad de la fuerza y la aceleración (Ecuación básica de la dinámica - Ley de Newton II) - La aceleración impartida a un punto material por la fuerza es directamente proporcional a la fuerza e inversamente proporcional a la masa de este punto: o Aquí m es la masa del punto (una medida de inercia), medida en kg, numéricamente igual al peso dividido por la aceleración de la gravedad: F es la fuerza actuante, medida en N (1 N imparte una aceleración de 1 m/s2 a un punto de masa 1 kg, 1 N \u003d 1 / 9.81 kg-s). ■ Dinámica de un sistema mecánico - estudia el movimiento de un conjunto de puntos materiales y cuerpos sólidos, unidos por las leyes generales de interacción, teniendo en cuenta las fuerzas que provocan este movimiento. ■ Mecánica analítica: estudia el movimiento de sistemas mecánicos no libres utilizando métodos analíticos. 1

4 diapositivas

Clase 1 (continuación - 1.2) Ecuaciones diferenciales de movimiento de un punto material: - ecuación diferencial de movimiento de un punto en forma vectorial. - ecuaciones diferenciales de movimiento puntual en forma de coordenadas. Este resultado puede obtenerse por proyección formal de la ecuación diferencial vectorial (1). Después de agrupar, la relación vectorial se descompone en tres ecuaciones escalares: En forma de coordenadas: Usamos la relación del vector de radio con coordenadas y el vector de fuerza con proyecciones: ecuación diferencial de movimiento en ejes de coordenadas naturales (en movimiento): o: - ecuaciones naturales del movimiento de un punto. ■ Ecuación básica de la dinámica: - Corresponde a la forma vectorial de especificar el movimiento de un punto. ■ La ley de independencia de la acción de las fuerzas - La aceleración de un punto material bajo la acción de varias fuerzas es igual a la suma geométrica de las aceleraciones de un punto por la acción de cada una de las fuerzas por separado: o La ley es válida para cualquier estado cinemático de los cuerpos. Las fuerzas de interacción, al ser aplicadas a diferentes puntos (cuerpos) no están equilibradas. ■ La ley de igualdad de acción y reacción (ley de Newton III) - Cada acción corresponde a una reacción igual y de dirección opuesta: 2

5 diapositivas

Dos problemas principales de dinámica: 1. Problema directo: El movimiento está dado (ecuaciones de movimiento, trayectoria). Se requiere determinar las fuerzas bajo cuya acción se produce un movimiento dado. 2. Problema inverso: Se dan las fuerzas bajo cuya acción se produce el movimiento. Se requiere para encontrar parámetros de movimiento (ecuaciones de movimiento, trayectoria de movimiento). Ambos problemas se resuelven utilizando la ecuación básica de la dinámica y su proyección sobre los ejes de coordenadas. Si se considera el movimiento de un punto no libre, entonces, como en estática, se usa el principio de liberación de enlaces. Como resultado de la reacción, los enlaces se incluyen en la composición de las fuerzas que actúan sobre el punto material. La solución del primer problema está relacionada con las operaciones de diferenciación. La solución del problema inverso requiere la integración de las ecuaciones diferenciales correspondientes, y esto es mucho más difícil que la diferenciación. El problema inverso es más difícil que el problema directo. La solución del problema directo de la dinámica - veamos ejemplos: Ejemplo 1. Una cabina con un peso G de un ascensor es levantada por un cable con una aceleración a . Determinar la tensión del cable. 1. Seleccione un objeto (la cabina del ascensor avanza y se puede considerar como un punto material). 2. Descartamos la conexión (cable) y la reemplazamos con la reacción R. 3. Compone la ecuación básica de la dinámica: Determina la reacción del cable: Determina la tensión del cable: Con un movimiento uniforme de la cabina ay = 0 y la la tensión del cable es igual al peso: T = G. Cuando el cable se rompe T = 0 y la aceleración de la cabina es igual a la aceleración de caída libre: ay = -g. 3 4. Proyectamos la ecuación básica de la dinámica sobre el eje y: y Ejemplo 2. Un punto de masa m se mueve a lo largo de una superficie horizontal (el plano Oxy) según las ecuaciones: x = a coskt, y = b coskt. Determine la fuerza que actúa sobre el punto. 1. Seleccione un objeto (punto material). 2. Descartamos la conexión (plano) y la reemplazamos con la reacción N. 3. Agregamos al sistema de fuerzas una fuerza desconocida F. 4. Componemos la ecuación básica de la dinámica: 5. Proyectamos la ecuación básica de la dinámica sobre la x , ejes y: Determine las proyecciones de fuerza: Módulo de fuerza: Cosenos directores: Por lo tanto, la magnitud de la fuerza es proporcional a la distancia del punto al centro de coordenadas y está dirigida hacia el centro a lo largo de la línea que conecta el punto con el centro . La trayectoria del movimiento del punto es una elipse centrada en el origen: O r Clase 1 (continuación - 1.3)

6 diapositivas

Clase 1 (continuación 1.4) Ejemplo 3: Una carga de peso G está suspendida de un cable de longitud l y se mueve a lo largo de una trayectoria circular en un plano horizontal con cierta velocidad. El ángulo de desviación del cable de la vertical es igual a. Determine la tensión del cable y la velocidad de la carga. 1. Seleccione un objeto (carga). 2. Deseche la conexión (cuerda) y reemplácela con la reacción R. 3. Componga la ecuación principal de la dinámica: A partir de la tercera ecuación, determine la reacción del cable: Determine la tensión del cable: Sustituya el valor de la reacción del cable, la aceleración normal en la segunda ecuación y determine la velocidad de la carga: 4. Proyecte la ecuación principal dinámica del eje,n,b: Ejemplo 4: Un automóvil de peso G se mueve sobre un puente convexo (el radio de curvatura es R ) con velocidad V. Determine la presión del automóvil sobre el puente. 1. Seleccionamos un objeto (un automóvil, despreciamos las dimensiones y lo consideramos como un punto). 2. Descartamos la conexión (superficie rugosa) y la reemplazamos con las reacciones N y la fuerza de fricción Ffr. 3. Componemos la ecuación básica de la dinámica: 4. Proyectamos la ecuación básica de la dinámica sobre el eje n: A partir de aquí determinamos la reacción normal: Determinamos la presión del carro sobre el puente: A partir de aquí podemos determinar la velocidad correspondiente a la presión cero en el puente (Q = 0): 4

7 diapositivas

Lección 2 Después de sustituir los valores encontrados de las constantes, obtenemos: Así, bajo la acción de un mismo sistema de fuerzas, un punto material puede realizar toda una clase de movimientos determinados por las condiciones iniciales. Las coordenadas iniciales tienen en cuenta la posición inicial del punto. La velocidad inicial, dada por las proyecciones, tiene en cuenta la influencia en su movimiento a lo largo de la sección considerada de la trayectoria de las fuerzas que actuaron en el punto antes de llegar a esta sección, es decir estado cinemático inicial. Solución del problema inverso de la dinámica - En el caso general del movimiento de un punto, las fuerzas que actúan sobre el punto son variables que dependen del tiempo, las coordenadas y la velocidad. El movimiento de un punto se describe mediante un sistema de tres ecuaciones diferenciales de segundo orden: Después de integrar cada una de ellas, quedarán seis constantes C1, C2,…., C6: Los valores de las constantes C1, C2,… ., C6 se encuentran a partir de seis condiciones iniciales en t = 0: Ejemplo 1 de solución del problema inverso: Un punto material libre de masa m se mueve bajo la acción de una fuerza F, la cual es constante en magnitud y magnitud. . En el momento inicial, la velocidad del punto era v0 y coincidía en dirección con la fuerza. Determinar la ecuación de movimiento de un punto. 1. Componemos la ecuación básica de la dinámica: 3. Rebajamos el orden de la derivada: 2. Elegimos el sistema de referencia cartesiano, dirigiendo el eje x en la dirección de la fuerza y proyectamos sobre este eje la ecuación principal de la dinámica: o xyz 4. Separe las variables: 5. Calcule las integrales de ambas partes de la ecuación: 6. Representemos la proyección de velocidad como la derivada temporal de la coordenada: 8. Calcule las integrales de ambas partes de la ecuación: 7. Separe las variables: 9. Para determinar los valores de las constantes C1 y C2, usamos las condiciones iniciales t = 0, vx = v0, x = x0: Como resultado, obtenemos la ecuación de movimiento uniformemente variable (a lo largo de la eje x): 5

8 diapositivas

Instrucciones generales para la resolución de problemas directos e inversos. Procedimiento de solución: 1. Compilación de la ecuación diferencial de movimiento: 1.1. Elija un sistema de coordenadas: rectangular (fijo) con una trayectoria de movimiento desconocida, natural (en movimiento) con una trayectoria conocida, por ejemplo, un círculo o una línea recta. EN último caso se puede utilizar una coordenada rectilínea. El punto de referencia debe combinarse con la posición inicial del punto (en t = 0) o con la posición de equilibrio del punto, si existe, por ejemplo, cuando el punto fluctúa. 6 1.2. Dibuja un punto en una posición correspondiente a un momento arbitrario en el tiempo (para t > 0) de modo que las coordenadas sean positivas (s > 0, x > 0). También suponemos que la proyección de velocidad en esta posición también es positiva. En el caso de oscilaciones, la proyección de la velocidad cambia de signo, por ejemplo, al volver a la posición de equilibrio. Aquí se debe suponer que en el momento considerado el punto se aleja de la posición de equilibrio. La implementación de esta recomendación es importante en el futuro cuando se trabaje con fuerzas de resistencia que dependan de la velocidad. 1.3. Libere el punto material de los enlaces, reemplace su acción con reacciones, agregue fuerzas activas. 1.4. Escribir la ley básica de la dinámica en forma de vector, proyectar sobre ejes seleccionados, expresar fuerzas dadas o reactivas en términos de tiempo, coordenadas o variables de velocidad, si dependen de ellas. 2. Solución de ecuaciones diferenciales: 2.1. Reduzca la derivada si la ecuación no se reduce a la forma canónica (estándar). por ejemplo: o 2.2. Separar variables, por ejemplo: o 2.4. Calcula las integrales indefinidas en los lados izquierdo y derecho de la ecuación, por ejemplo: 2.3. Si hay tres variables en la ecuación, entonces haga un cambio de variables, por ejemplo: y luego separe las variables. Comentario. en lugar de calcular Integrales indefinidas es posible calcular integrales definidas con un límite superior variable. Los límites inferiores representan los valores iniciales de las variables (condiciones iniciales) Entonces no hay necesidad de encontrar por separado la constante, que se incluye automáticamente en la solución, por ejemplo: Usando las condiciones iniciales, por ejemplo, t = 0 , vx = vx0, determine la constante de integración: 2.5. Exprese la velocidad en términos de la derivada temporal de la coordenada, por ejemplo, y repita los pasos 2.2 -2.4 Nota. Si la ecuación se reduce a una forma canónica que tiene una solución estándar, entonces esto es solución llave en mano y se usa Las constantes de integración todavía se encuentran a partir de las condiciones iniciales. Ver, por ejemplo, oscilaciones (lección 4, p. 8). Clase 2 (continuación 2.2)

9 diapositivas

Lección 2 (continuación 2.3) Ejemplo 2 de resolución del problema inverso: La fuerza depende del tiempo. Una carga de peso P comienza a moverse a lo largo de una superficie horizontal lisa bajo la acción de una fuerza F, cuya magnitud es proporcional al tiempo (F = kt). Determine la distancia recorrida por la carga en el tiempo t. 3. Componer la ecuación básica de la dinámica: 5. Reducir el orden de la derivada: 4. Proyectar la ecuación básica de la dinámica en el eje x: o 7 6. Separar las variables: 7. Calcular las integrales de ambas partes de la ecuación: 9. Representar la proyección de la velocidad como la derivada de la coordenada con respecto al tiempo: 10. Calcular las integrales de ambas partes de la ecuación: 9. Separar las variables: 8. Determinar el valor de la constante C1 a partir de la condición inicial t = 0, vx = v0=0: Como resultado, obtenemos la ecuación de movimiento (sobre el eje x), que da el valor de la distancia recorrida en el tiempo t: 1. Elegimos el sistema de referencia (cartesiano coordenadas) para que el cuerpo tenga una coordenada positiva: 2. Tomamos el objeto de movimiento como un punto material (el cuerpo avanza), lo liberamos de la conexión (plano de referencia) y lo reemplazamos con la reacción (reacción normal de un superficie lisa): 11. Determinar el valor de la constante C2 a partir de la condición inicial t = 0, x = x0=0: Ejemplo 3 de resolución del problema inverso: La fuerza depende de la coordenada. Un punto material de masa m es lanzado hacia arriba desde la superficie terrestre con una velocidad v0. La fuerza de gravedad de la Tierra es inversamente proporcional al cuadrado de la distancia del punto al centro de gravedad (el centro de la Tierra). Determine la dependencia de la velocidad con la distancia y al centro de la Tierra. 1. Elegimos el sistema de referencia (coordenadas cartesianas) para que el cuerpo tenga una coordenada positiva: 2. Componemos la ecuación básica de la dinámica: 3. Proyectamos la ecuación básica de la dinámica en el eje y: o El coeficiente de proporcionalidad puede se puede encontrar usando el peso de un punto en la superficie de la Tierra: R Por lo tanto, el diferencial de la ecuación se ve como: o 4. Disminuir el orden de la derivada: 5. Cambiar la variable: 6. Separar las variables: 7. Calcular el integrales de ambos lados de la ecuación: 8. Sustituye los límites: Como resultado, obtenemos una expresión para la velocidad en función de la coordenada y: La altura máxima de vuelo se puede encontrar igualando la velocidad a cero: La altitud máxima de vuelo cuando el denominador se vuelve cero: De aquí, al establecer el radio de la Tierra y la aceleración de caída libre, se obtiene II velocidad espacial:

10 diapositivas

Lección 2 (continuación 2.4) Ejemplo 2 de resolución del problema inverso: La fuerza depende de la velocidad. Un barco de masa m tenía una velocidad v0. La resistencia del agua al movimiento del barco es proporcional a la velocidad. Determine el tiempo que tarda la velocidad del barco en reducirse a la mitad después de apagar el motor, así como la distancia recorrida por el barco hasta detenerse por completo. 8 1. Elegimos un sistema de referencia (coordenadas cartesianas) para que el cuerpo tenga una coordenada positiva: 2. Tomamos el objeto de movimiento como un punto material (el barco avanza), lo liberamos de ataduras (agua) y lo reemplazamos con una reacción (fuerza de flotación - fuerza de Arquímedes), y también la fuerza de resistencia al movimiento. 3. Añadir fuerza activa (gravedad). 4. Componemos la ecuación principal de la dinámica: 5. Proyectamos la ecuación principal de la dinámica sobre el eje x: o 6. Bajamos el orden de la derivada: 7. Separamos las variables: 8. Calculamos las integrales de ambas partes de la ecuación: 9. Sustituimos los límites: Se obtiene una expresión que relaciona la velocidad y el tiempo t, a partir de la cual se puede determinar el tiempo de movimiento: El tiempo de movimiento, durante el cual la velocidad se reducirá a la mitad: Es interesante notar que cuando la velocidad se aproxima a cero, el tiempo de movimiento tiende a infinito, es decir la velocidad final no puede ser cero. ¿Por qué no "movimiento perpetuo"? Sin embargo, en este caso, la distancia recorrida hasta la parada es un valor finito. Para determinar la distancia recorrida, recurrimos a la expresión obtenida después de bajar el orden de la derivada y hacer un cambio de variable: Después de integrar y sustituir los límites, obtenemos: Distancia recorrida hasta el tope: ■ Movimiento de un punto lanzado a una ángulo con el horizonte en un campo de gravedad uniforme sin tener en cuenta la resistencia del aire Eliminando el tiempo de las ecuaciones de movimiento, obtenemos la ecuación de la trayectoria: El tiempo de vuelo se determina igualando la coordenada y a cero: El rango de vuelo se determina sustituyendo el tiempo de vuelo:

11 diapositivas

Lección 3 Oscilaciones rectilíneas de un punto material - El movimiento oscilatorio de un punto material ocurre bajo la condición de que exista una fuerza restauradora que tiende a devolver el punto a la posición de equilibrio para cualquier desviación de esta posición. 9 Hay una fuerza restauradora, la posición de equilibrio es estable Sin fuerza restauradora, la posición de equilibrio es inestable Sin fuerza restauradora, la posición de equilibrio es indiferente Siempre está dirigido hacia la posición de equilibrio, el valor es directamente proporcional al alargamiento lineal (acortamiento) del resorte, que es igual a la desviación del cuerpo de la posición de equilibrio: c es el coeficiente de rigidez del resorte, numéricamente igual a la fuerza bajo la cual el resorte cambia su longitud en uno, medida en N/m en el sistema SI. x y O Tipos de vibraciones de un punto material: 1. Vibraciones libres (sin tener en cuenta la resistencia del medio). 2. Oscilaciones libres teniendo en cuenta la resistencia del medio (oscilaciones amortiguadas). 3. Vibraciones forzadas. 4. Oscilaciones forzadas teniendo en cuenta la resistencia del medio. ■ Oscilaciones libres: ocurren bajo la acción de una fuerza restauradora solamente. Escribamos la ley básica de la dinámica: Elijamos un sistema de coordenadas centrado en la posición de equilibrio (punto O) y proyectemos la ecuación en el eje x: Llevemos la ecuación resultante a la forma estándar (canónica): Esta ecuación es homogénea ecuación diferencial lineal de segundo orden, cuya forma de solución está determinada por las raíces de la característica de la ecuación obtenida por sustitución universal: Las raíces de la ecuación característica son imaginarias e iguales: La solución general de la ecuación diferencial tiene la forma: Velocidad puntual: Condiciones iniciales: Defina las constantes: Entonces, la ecuación de vibraciones libres tiene la forma: La ecuación puede representarse mediante una expresión de un solo término: donde a es la amplitud, - fase inicial. Las nuevas constantes ay - están relacionadas con las constantes C1 y C2 por las relaciones: Definamos ay: La razón de la ocurrencia de oscilaciones libres es el desplazamiento inicial x0 y/o la velocidad inicial v0.

12 diapositivas

10 Clase 3 (continuación 3.2) Oscilaciones amortiguadas de un punto material - El movimiento oscilatorio de un punto material ocurre en presencia de una fuerza restauradora y una fuerza de resistencia al movimiento. Se determina la dependencia de la fuerza de resistencia al movimiento sobre el desplazamiento o la velocidad. naturaleza física entorno o comunicación que impide el movimiento. La dependencia más simple es una dependencia lineal de la velocidad (resistencia viscosa): - coeficiente de viscosidad xy O Ecuación básica de la dinámica: Proyección de la ecuación de la dinámica en el eje: Llevemos la ecuación a la forma estándar: donde La ecuación característica tiene raíces: La solución general de esta ecuación diferencial tiene una forma diferente dependiendo de los valores de las raíces: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - caso de alta resistencia viscosa: - raíces reales, diferentes. o - estas funciones son aperiódicas: 3. n = k: - las raíces son reales, múltiples. estas funciones también son aperiódicas:

13 diapositivas

Tema 3 (continuación 3.3) Clasificación de soluciones de oscilaciones libres. Conexiones de resorte. dureza equivalente. y y 11 Dif. Carácter de la ecuación. Ecuación Raíces char. ecuación Resolver ecuación diferencial Graficar nk n=k

14 diapositivas

Lección 4 Vibraciones forzadas de un punto material - Junto con la fuerza restauradora, actúa una fuerza que cambia periódicamente, llamada fuerza perturbadora. La fuerza perturbadora puede tener una naturaleza diferente. Por ejemplo, en un caso particular, el efecto inercial de una masa desequilibrada m1 de un rotor giratorio provoca proyecciones de fuerza que cambian armónicamente: La ecuación principal de la dinámica: La proyección de la ecuación de la dinámica en el eje: Traigamos la ecuación al estándar forma: 12 La solución de esta ecuación diferencial no homogénea consta de dos partes x = x1 + x2: x1 es la solución general de la ecuación homogénea correspondiente y x2 es una solución particular ecuación no homogénea: Seleccionamos una solución particular en la forma del lado derecho: La igualdad resultante debe ser satisfecha para cualquier t . Entonces: o Así, con la acción simultánea de las fuerzas restauradoras y perturbadoras, el punto material realiza un movimiento oscilatorio complejo, que es el resultado de la suma (superposición) de vibraciones libres (x1) y forzadas (x2). Si p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (oscilaciones forzadas de alta frecuencia), entonces la fase de las oscilaciones es opuesta a la fase de la fuerza perturbadora:

15 diapositivas

Lección 4 (continuación 4.2) 13 Coeficiente dinámico: la relación entre la amplitud de las oscilaciones forzadas y la desviación estática de un punto bajo la acción de una fuerza constante H = const: La amplitud de las oscilaciones forzadas: La desviación estática se puede encontrar a partir de la ecuación de equilibrio: Aquí: De aquí: Así, en p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (alta frecuencia de oscilaciones forzadas) coeficiente dinámico: Resonancia - ocurre cuando la frecuencia de las oscilaciones forzadas coincide con la frecuencia de las oscilaciones naturales (p = k). Esto ocurre con mayor frecuencia al iniciar y detener la rotación de rotores mal equilibrados montados sobre suspensiones elásticas. La ecuación diferencial de oscilaciones con frecuencias iguales: No se puede tomar una solución particular en la forma del lado derecho, porque se obtendrá una solución linealmente dependiente (ver la solución general). Solución general: Sustituir en la ecuación diferencial: Tomemos una solución particular en la forma y calculemos las derivadas: Así se obtiene la solución: o Las oscilaciones forzadas en resonancia tienen una amplitud que aumenta indefinidamente en proporción al tiempo. Influencia de la resistencia al movimiento durante vibraciones forzadas. La ecuación diferencial en presencia de resistencia viscosa tiene la forma: La solución general se selecciona de la tabla (Clase 3, p. 11) dependiendo de la relación de n y k (ver). Tomamos una solución particular en la forma y calculamos las derivadas: Sustituir en la ecuación diferencial: Igualando los coeficientes al mismo funciones trigonométricas obtenemos un sistema de ecuaciones: Al elevar ambas ecuaciones a una potencia y sumarlas, obtenemos la amplitud de las oscilaciones forzadas: Al dividir la segunda ecuación entre la primera, obtenemos el desfase de las oscilaciones forzadas: Así, la ecuación de movimiento para oscilaciones forzadas, teniendo en cuenta la resistencia al movimiento, por ejemplo, en n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 diapositivas

Lección 5 Movimiento relativo de un punto material: supongamos que el sistema de coordenadas en movimiento (no inercial) Oxyz se mueve de acuerdo con alguna ley relativa al sistema de coordenadas fijo (inercial) O1x1y1z1. El movimiento de un punto material M (x, y, z) relativo al sistema móvil Oxyz es relativo, relativo al sistema inmóvil O1x1y1z1 es absoluto. El movimiento del sistema móvil Oxyz relativo al sistema fijo O1x1y1z1 es un movimiento portátil. 14 z x1 y1 z1 O1 xy M xyz O Ecuación básica de la dinámica: Aceleración absoluta de un punto: Sustituya la aceleración absoluta de un punto en la ecuación principal de la dinámica: Transfiramos los términos con aceleración de traslación y de Coriolis al lado derecho: La Los términos transferidos tienen la dimensión de fuerzas y se consideran como las fuerzas de inercia correspondientes, iguales: Entonces el movimiento relativo del punto puede considerarse absoluto si sumamos las fuerzas de inercia de traslación y de Coriolis a las fuerzas actuantes: En proyecciones sobre los ejes del sistema de coordenadas en movimiento, tenemos: la rotación es uniforme, entonces εe = 0: 2. Movimiento curvilíneo traslacional: Si el movimiento es rectilíneo, entonces = : Si el movimiento es rectilíneo y uniforme, entonces el sistema en movimiento es inercial y el relativo el movimiento puede ser considerado como absoluto: ningún fenómeno mecánico puede detectar un uniforme rectilíneo movimiento (principio de relatividad de la mecánica clásica). Influencia de la rotación de la Tierra en el equilibrio de los cuerpos - Supongamos que el cuerpo está en equilibrio sobre la superficie de la Tierra en una latitud arbitraria φ (paralelos). La Tierra gira alrededor de su eje de oeste a este con una velocidad angular: El radio de la Tierra es de unos 6370 km. S R- reacción completa superficie irregular. G - fuerza de atracción de la Tierra hacia el centro. Ф - fuerza centrífuga de inercia. Condición de equilibrio relativo: La resultante de las fuerzas de atracción e inercia es la fuerza de gravedad (peso): La magnitud de la fuerza de gravedad (peso) sobre la superficie de la Tierra es P = mg. La fuerza centrífuga de inercia es una pequeña fracción de la fuerza de gravedad: La desviación de la fuerza de gravedad de la dirección de la fuerza de atracción también es pequeña: Por lo tanto, la influencia de la rotación de la Tierra en el equilibrio de los cuerpos es extremadamente pequeña. y no se tiene en cuenta en los cálculos prácticos. El valor máximo de la fuerza de inercia (en φ = 0 - en el ecuador) es solo 0.00343 del valor de la gravedad

17 diapositivas

Lección 5 (continuación 5.2) 15 Influencia de la rotación de la Tierra en el movimiento de cuerpos en el campo gravitatorio de la Tierra - Supongamos que un cuerpo cae a la Tierra desde una cierta altura H sobre la superficie de la Tierra en la latitud φ. Elijamos un marco de referencia móvil, rígidamente conectado con la Tierra, que dirija los ejes x, y tangencialmente al paralelo y al meridiano: La ecuación del movimiento relativo: Aquí se tiene en cuenta la pequeñez fuerza centrífuga inercia en comparación con la gravedad. Así, la fuerza de gravedad se identifica con la fuerza de gravedad. Además, asumimos que la gravedad se dirige perpendicularmente a la superficie de la Tierra debido a la pequeñez de su desviación, como se discutió anteriormente. La aceleración de Coriolis es igual y está dirigida paralelamente al eje y hacia el oeste. La fuerza de inercia de Coriolis está dirigida en la dirección opuesta. Proyectamos la ecuación de movimiento relativo sobre el eje: La solución de la primera ecuación da: Condiciones iniciales: La solución de la tercera ecuación da: Condiciones iniciales: La tercera ecuación toma la forma: Condiciones iniciales: Su solución da: La solución resultante muestra que el cuerpo se desvía hacia el este cuando cae. Calculemos el valor de esta desviación, por ejemplo, al caer desde una altura de 100 m. Hallamos el tiempo de caída a partir de la solución de la segunda ecuación: Por lo tanto, la influencia de la rotación de la Tierra en el movimiento de los cuerpos es extremadamente pequeña. para alturas y velocidades prácticas y no se tiene en cuenta en los cálculos técnicos. La solución de la segunda ecuación también implica la existencia de una velocidad a lo largo del eje y, que también debe causar y causa la correspondiente aceleración y la fuerza de inercia de Coriolis. La influencia de esta velocidad y la fuerza de inercia asociada a ella sobre el cambio de movimiento será incluso menor que la fuerza de inercia de Coriolis considerada asociada a la velocidad vertical.

18 diapositivas

Tema 6 Dinámica de un sistema mecánico. Sistema de puntos materiales o sistema mecánico - Conjunto de puntos materiales o puntos materiales, unidos por leyes generales de interacción (la posición o movimiento de cada punto o cuerpo depende de la posición y movimiento de todos los demás) Sistema puntos gratis- cuyo movimiento no está limitado por ninguna conexión (por ejemplo, un sistema planetario en el que los planetas se consideran puntos materiales). Un sistema de puntos no libres o un sistema mecánico no libre: el movimiento de puntos o cuerpos materiales está limitado por las restricciones impuestas al sistema (por ejemplo, un mecanismo, una máquina, etc.). 16 Fuerzas que actúan sobre el sistema. Además de la clasificación de fuerzas previamente existente (fuerzas activas y reactivas), se introduce una nueva clasificación de fuerzas: 1. Fuerzas externas (e) - que actúan sobre puntos y cuerpos del sistema desde puntos o cuerpos que no forman parte de este sistema. 2. Fuerzas internas (i) - fuerzas de interacción entre puntos materiales o cuerpos incluidos en el sistema dado. Una misma fuerza puede ser tanto fuerza externa como interna. Todo depende de qué sistema mecánico se considere. Por ejemplo: En el sistema del Sol, la Tierra y la Luna, todas las fuerzas gravitatorias entre ellos son internas. Al considerar el sistema de la Tierra y la Luna, las fuerzas gravitatorias aplicadas desde el lado del Sol son externas: CZL Basado en la ley de acción y reacción, cada fuerza interna Fk corresponde a otra fuerza interna Fk', igual en valor absoluto y opuesta en dirección. De aquí se siguen dos propiedades notables de las fuerzas internas: El vector principal de todas las fuerzas internas del sistema es igual a cero: El momento principal de todas las fuerzas internas del sistema relativo a cualquier centro es igual a cero: O en proyecciones sobre la coordenada ejes: Nota. Aunque estas ecuaciones son similares a las ecuaciones de equilibrio, no lo son, ya que las fuerzas internas se aplican a varios puntos o cuerpos del sistema y pueden hacer que estos puntos (cuerpos) se muevan entre sí. De estas ecuaciones se sigue que las fuerzas internas no afectan el movimiento de un sistema considerado como un todo. El centro de masa del sistema de puntos materiales. Para describir el movimiento del sistema como un todo, se introduce un punto geométrico, llamado centro de masa, cuyo radio vector está determinado por la expresión, donde M es la masa de todo el sistema: O en proyecciones sobre la coordenada ejes: Las fórmulas para el centro de masa son similares a las del centro de gravedad. Sin embargo, el concepto de centro de masa es más general, ya que no está relacionado con las fuerzas de gravedad o las fuerzas de gravedad.

19 diapositiva

Lección 6 (continuación 6.2) 17 Teorema sobre el movimiento del centro de masa del sistema - Considere un sistema de n puntos materiales. Dividimos las fuerzas aplicadas a cada punto en externas e internas y las reemplazamos con las correspondientes resultantes Fke y Fki. Escribamos para cada punto la ecuación básica de la dinámica: o Sumemos estas ecuaciones sobre todos los puntos: En el lado izquierdo de la ecuación, introduciremos las masas bajo el signo de la derivada y sustituiremos la suma de las derivadas por la derivada de la suma: De la definición del centro de masa: Sustituir en la ecuación resultante: obtenemos o: El producto de la masa del sistema y la aceleración de su centro de masa es igual al vector principal de fuerzas externas. En proyecciones sobre los ejes de coordenadas: El centro de masas del sistema se desplaza como un punto material de masa igual a la masa de todo el sistema, sobre el que se aplican todas las fuerzas externas que actúan sobre el sistema. Consecuencias del teorema sobre el movimiento del centro de masa del sistema (leyes de conservación): 1. Si en el intervalo de tiempo el vector principal de las fuerzas externas del sistema es cero, Re = 0, entonces la velocidad del centro de masa es constante, vC = const (el centro de masa se mueve uniformemente rectilíneo - la ley de conservación del centro de movimiento de masa). 2. Si en el intervalo de tiempo la proyección del vector principal de las fuerzas externas del sistema sobre el eje x es igual a cero, Rxe = 0, entonces la velocidad del centro de masa a lo largo del eje x es constante, vCx = const (el centro de masa se mueve uniformemente a lo largo del eje). Declaraciones similares son ciertas para los ejes y y z. Ejemplo: Dos personas de masas m1 y m2 están en un bote de masa m3. En el momento inicial del tiempo, el barco con personas estaba en reposo. Determine el desplazamiento del bote si una persona de masa m2 se moviera hacia la proa del bote a una distancia a. 3. Si en el intervalo de tiempo el vector principal de las fuerzas externas del sistema es igual a cero, Re = 0, y en el momento inicial la velocidad del centro de masa es cero, vC = 0, entonces el radio vector de el centro de masa permanece constante, rC = const (el centro de masa está en reposo es la ley de conservación de la posición del centro de masa). 4. Si en el intervalo de tiempo la proyección del vector principal de las fuerzas externas del sistema sobre el eje x es igual a cero, Rxe = 0, y en el momento inicial la velocidad del centro de masas a lo largo de este eje es cero , vCx = 0, entonces la coordenada del centro de masa a lo largo del eje x permanece constante, xC = const (el centro de masa no se mueve a lo largo de este eje). Declaraciones similares son ciertas para los ejes y y z. 1. El objeto del movimiento (un bote con personas): 2. Descartamos conexiones (agua): 3. Reemplazamos la conexión con una reacción: 4. Sumamos fuerzas activas: 5. Escribe el teorema sobre el centro de masa: Proyecte en el eje x: O Determine qué tan lejos necesita transferir a una persona de masa m1, para que el bote permanezca en su lugar: El bote se moverá una distancia l en la dirección opuesta.

20 diapositivas

Lección 7 El impulso de fuerza es una medida de interacción mecánica que caracteriza la transferencia de movimiento mecánico de las fuerzas que actúan sobre un punto durante un período de tiempo determinado: 18 En proyecciones sobre ejes de coordenadas: En el caso de una fuerza constante: En proyecciones sobre ejes coordenados: al punto de fuerza en el mismo intervalo de tiempo: Multiplicar por dt: Integrar sobre un intervalo de tiempo dado: El momento de un punto es una medida del movimiento mecánico, determinada por un vector igual al producto de la masa del punto y su vector velocidad: Teorema de la variación de la cantidad de movimiento del sistema - Considere el sistema n puntos materiales. Dividimos las fuerzas aplicadas a cada punto en externas e internas y las reemplazamos con las correspondientes resultantes Fke y Fki. Escribamos para cada punto la ecuación básica de la dinámica: o Cantidad de movimiento de un sistema de puntos materiales - la suma geométrica de las cantidades de movimiento de los puntos materiales: Por definición del centro de masa: El vector del momento del sistema es igual al producto de la masa de todo el sistema y el vector de velocidad del centro de masa del sistema. Entonces: En proyecciones sobre los ejes de coordenadas: La derivada temporal del vector momento del sistema es igual al vector principal de las fuerzas externas del sistema. Sumemos estas ecuaciones sobre todos los puntos: En el lado izquierdo de la ecuación, introducimos las masas bajo el signo de la derivada y reemplazamos la suma de las derivadas con la derivada de la suma: De la definición del momento del sistema: En proyecciones sobre los ejes de coordenadas:

21 diapositivas

Teorema de Euler - Aplicación del teorema de la variación de la cantidad de movimiento del sistema al movimiento continuo(agua) . 1. Seleccionamos como objeto de movimiento el volumen de agua ubicado en el canal curvilíneo de la turbina: 2. Descartamos las conexiones y reemplazamos su acción con reacciones (Rpov - la resultante de las fuerzas superficiales) 3. Agregamos fuerzas activas (Rb - la resultante de las fuerzas del cuerpo): 4. Escriba el teorema sobre el cambio en la cantidad de movimiento del sistema: La cantidad de movimiento del agua en los tiempos t0 y t1 se representará como sumas: Cambio en la cantidad de movimiento del agua en el intervalo de tiempo : Cambio en la cantidad de movimiento del agua en un intervalo de tiempo infinitesimal dt: , donde F1 F2 Tomando el producto de la densidad, el área de la sección transversal y la velocidad por segundo de masa, obtenemos: Sustituyendo el diferencial de la cantidad de movimiento del sistema en el teorema del cambio , obtenemos: Consecuencias del teorema sobre el cambio en el momento del sistema (leyes de conservación): 1. Si en el intervalo de tiempo el vector principal de las fuerzas externas del sistema es igual a cero, Re = 0, entonces el cantidad de movimiento del vector es constante, Q = const es la ley de conservación del momento del sistema). 2. Si en el intervalo de tiempo la proyección del vector principal de las fuerzas externas del sistema sobre el eje x es igual a cero, Rxe = 0, entonces la proyección de la cantidad de movimiento del sistema sobre el eje x es constante, Qx = constante Declaraciones similares son ciertas para los ejes y y z. Clase 7 (continuación de 7.2) Ejemplo: Una granada de masa M, volando a una velocidad v, explotó en dos partes. La velocidad de uno de los fragmentos de masa m1 aumentó en la dirección del movimiento al valor v1. Determine la velocidad del segundo fragmento. 1. El objeto de movimiento (granada): 2. El objeto es un sistema libre, no hay conexiones y sus reacciones. 3. Suma las fuerzas activas: 4. Escribe el teorema del cambio de cantidad de movimiento: Proyecta sobre el eje: β Divide las variables e integra: La integral derecha es casi cero, porque tiempo de explosión t

22 diapositivas

Lección 7 (continuación 7.3) 20 El momento angular de un punto o el momento cinético del movimiento relativo a cierto centro es una medida del movimiento mecánico, determinada por un vector igual al vector producto del radio vector de un punto material y el vector de su cantidad de movimiento: El momento cinético de un sistema de puntos materiales con respecto a un centro determinado es geométrica la suma de los momentos del número de movimientos de todos los puntos materiales con respecto al mismo centro: En proyecciones sobre el eje: En proyecciones sobre el eje: Teorema sobre el cambio en el momento de la cantidad de movimiento del sistema - Considere un sistema de n puntos materiales. Dividimos las fuerzas aplicadas a cada punto en externas e internas y las reemplazamos con las correspondientes resultantes Fke y Fki. Escribamos para cada punto la ecuación básica de la dinámica: o Sumemos estas ecuaciones para todos los puntos: Reemplacemos la suma de las derivadas por la derivada de la suma: La expresión entre paréntesis es el momento del momento del sistema. A partir de aquí: Multiplicamos vectorialmente cada una de las igualdades por el radio vector de la izquierda: Veamos si es posible sacar el signo de la derivada fuera del producto vectorial: Así, tenemos: centro. En proyecciones sobre los ejes coordenados: La derivada del momento de la cantidad de movimiento del sistema con respecto a algún eje en el tiempo es igual al momento principal de las fuerzas externas del sistema con respecto al mismo eje.

23 diapositiva

Clase 8 21 ■ Consecuencias del teorema sobre el cambio en el momento angular del sistema (leyes de conservación): 1. Si en el intervalo de tiempo el vector del momento principal de las fuerzas externas del sistema con respecto a un cierto centro es igual a cero, MOe = 0, entonces el vector del momento angular del sistema relativo al mismo centro es constante, KO = const es la ley de conservación del momento del sistema). 2. Si en el intervalo de tiempo el momento principal de las fuerzas externas del sistema con respecto al eje x es igual a cero, Mxe = 0, entonces el momento angular del sistema con respecto al eje x es constante, Kx = const. Declaraciones similares son ciertas para los ejes y y z. 2. Momento de inercia de un cuerpo rígido respecto al eje: El momento de inercia de un punto material respecto al eje es igual al producto de la masa del punto por el cuadrado de la distancia del punto al eje. Momento de inercia de un cuerpo rígido respecto a un eje es igual a la suma los productos de la masa de cada punto y el cuadrado de la distancia de este punto al eje. ■ Elementos de la teoría de los momentos de inercia - Cuando movimiento rotatorio cuerpo rígido medida de inercia (resistencia a cambiar el movimiento) es el momento de inercia sobre el eje de rotación. Considere los conceptos básicos de la definición y los métodos para calcular los momentos de inercia. 1. Momento de inercia de un punto material con respecto al eje: En la transición de una pequeña masa discreta a una masa infinitamente pequeña de un punto, el límite de tal suma está determinado por la integral: momento de inercia axial de un cuerpo rígido . Además del momento de inercia axial de un cuerpo rígido, existen otros tipos de momentos de inercia: el momento de inercia centrífugo de un cuerpo rígido. Momento polar de inercia de un cuerpo rígido. 3. Teorema sobre los momentos de inercia de un cuerpo rígido sobre ejes paralelos - la fórmula para la transición a ejes paralelos: Momento de inercia sobre el eje de referencia Momentos estáticos de inercia sobre los ejes de referencia Masa del cuerpo Distancia entre los ejes z1 y z2 Así : los momentos son cero:

24 diapositivas

Lección 8 (continuación 8.2) 22 Momento de inercia de una barra uniforme de sección constante alrededor del eje: xz L Seleccione el volumen elemental dV = Adx a una distancia x: x dx Masa elemental: Para calcular el momento de inercia alrededor del eje central (que pasa por el centro de gravedad), basta cambiar la ubicación del eje y establecer los límites de integración (-L/2, L/2). Aquí demostramos la fórmula para la transición a ejes paralelos: zС 5. El momento de inercia de un cilindro sólido homogéneo sobre el eje de simetría: H dr r Destaquemos el volumen elemental dV = 2πrdrH (cilindro delgado de radio r) : Masa elemental: Aquí usamos la fórmula del volumen del cilindro V=πR2H. Para calcular el momento de inercia de un cilindro hueco (grueso), basta establecer los límites de integración de R1 a R2 (R2> R1): 6. El momento de inercia de un cilindro delgado con respecto al eje de simetría (t

25 diapositivas

Lección 8 (continuación 8.3) 23 ■ Ecuación diferencial de rotación de un cuerpo rígido alrededor de un eje: Escribamos un teorema sobre el cambio del momento angular de un cuerpo rígido que gira alrededor de un eje fijo: El momento de un cuerpo rígido que gira es: El momento de fuerzas externas sobre el eje de rotación es igual al torque (las reacciones y la fuerza no crean momentos de gravedad): Sustituimos el momento cinético y el torque en el teorema Ejemplo: Dos personas del mismo peso G1 = G2 cuelgan de una cuerda lanzada sobre un bloque macizo de peso G3 = G1/4. En algún momento, uno de ellos empezó a trepar por la cuerda con una velocidad relativa u. Determine la velocidad de elevación de cada persona. 1. Seleccione el objeto de movimiento (bloque con personas): 2. Deseche las conexiones (dispositivo de soporte del bloque): 3. Reemplace la conexión con reacciones (rodamiento): 4. Agregue fuerzas activas (gravedad): 5. Anote el teorema sobre el cambio del momento cinético del sistema con respecto al eje de rotación del bloque: R Dado que el momento de las fuerzas externas es igual a cero, el momento cinético debe permanecer constante: En el momento inicial de tiempo t = 0, hay estaba en equilibrio y Kz0 = 0. Después del comienzo del movimiento de una persona con respecto a la cuerda, todo el sistema comenzó a moverse, pero el momento cinético del sistema debe permanecer igual a cero: Kz = 0. El momento angular del es la suma de los momentos angulares de las personas y del bloque: Aquí v2 es la velocidad de la segunda persona, igual a la velocidad del cable, Ejemplo: Determinar el periodo de pequeñas oscilaciones libres de una varilla homogénea de masa M y longitud l, suspendido por un extremo a un eje fijo de rotación. O: En el caso de oscilaciones pequeñas senφ φ: Período de oscilación: Momento de inercia de la barra:

26 diapositivas

Lección 8 (continuación 8.4 - material adicional) 24 ■ Teoría elemental del giroscopio: Un giroscopio es un cuerpo rígido que gira alrededor del eje de simetría material, uno de cuyos puntos es fijo. Un giroscopio libre se fija de tal manera que su centro de masa permanece estacionario, y el eje de rotación pasa por el centro de masa y puede tomar cualquier posición en el espacio, es decir el eje de rotación cambia su posición como el eje de rotación del propio cuerpo durante el movimiento esférico. La suposición principal de la teoría aproximada (elemental) del giroscopio es que se considera que el vector de impulso (momento cinético) del rotor está dirigido a lo largo de su propio eje de rotación. Así, a pesar de que en el caso general el rotor participa en tres rotaciones, sólo se tiene en cuenta la velocidad angular de su propia rotación ω = dφ/dt. La base de esto es que en tecnología moderna el rotor del giroscopio gira a una velocidad angular del orden de 5000-8000 rad/s (alrededor de 50000-80000 rpm), mientras que las otras dos velocidades angulares asociadas con la precesión y nutación de su propio eje de rotación son decenas de miles de veces menos que esta velocidad. La propiedad principal de un giroscopio libre es que el eje del rotor mantiene la misma dirección en el espacio con respecto al sistema de referencia inercial (estelar) (demostrado por el péndulo de Foucault, que mantiene el plano de oscilación sin cambios con respecto a las estrellas, 1852). Esto se deduce de la ley de conservación del momento cinético relativo al centro de masa del rotor, siempre que se desprecie la fricción en los cojinetes de los ejes de suspensión del rotor, el marco exterior e interior: Acción de fuerza sobre el eje de un libre giroscopio. En el caso de una fuerza aplicada al eje del rotor, el momento de las fuerzas externas con respecto al centro de masa no es igual a cero: ω ω С fuerza, y hacia el vector del momento de esta fuerza, es decir girará no sobre el eje x (suspensión interna), sino sobre el eje y (suspensión externa). Al terminar la fuerza, el eje del rotor permanecerá en la misma posición, correspondiente al último tiempo de la fuerza, porque a partir de este momento, el momento de las fuerzas externas vuelve a ser igual a cero. En el caso de una acción de fuerza (impacto) de corta duración, el eje del giroscopio prácticamente no cambia de posición. Así, la rápida rotación del rotor le da al giroscopio la capacidad de contrarrestar las influencias aleatorias que buscan cambiar la posición del eje de rotación del rotor, y con una acción constante de la fuerza, mantiene la posición del plano perpendicular a la fuerza de actuación en la que se encuentra el eje del rotor. Estas propiedades se utilizan en el funcionamiento de los sistemas de navegación inercial.

Conferencias sobre Mecánica Teórica

Dinámica de puntos

Conferencia 1

Conceptos básicos de dinámica.

En la sección Dinámica se estudia el movimiento de los cuerpos bajo la acción de fuerzas aplicadas sobre ellos. Por lo tanto, además de los conceptos que se introdujeron en la sección Cinemática, aquí es necesario utilizar nuevos conceptos que reflejen las especificidades del impacto de las fuerzas sobre varios cuerpos y la respuesta de los cuerpos a estos impactos. Consideremos el principal de estos conceptos.

Una fuerza

La fuerza es el resultado cuantitativo del impacto sobre un cuerpo dado por parte de otros cuerpos. La fuerza es una cantidad vectorial (Fig. 1).

Punto A del comienzo del vector fuerza F llamado punto de aplicación de la fuerza. La recta MN sobre la que se encuentra el vector fuerza se llama línea de fuerza. La longitud del vector fuerza, medida en cierta escala, se llama valor numérico o módulo del vector fuerza. El módulo de fuerza se denota como o . La acción de una fuerza sobre un cuerpo se manifiesta en su deformación, si el cuerpo está estacionario, o en impartirle aceleración cuando el cuerpo se mueve. Sobre estas manifestaciones de fuerza se basa el dispositivo de varios instrumentos (dinamómetros o dinamómetros) para medir fuerzas.

b) sistema de fuerzas

El conjunto considerado de fuerzas se forma sistema de fuerza. Cualquier sistema que consta de n fuerzas se puede escribir de la siguiente forma:

c) cuerpo libre

Un cuerpo que puede moverse en el espacio en cualquier dirección sin experimentar interacción directa (mecánica) con otros cuerpos se llama gratis o aislado. La influencia de uno u otro sistema de fuerzas sobre un cuerpo sólo puede aclararse si este cuerpo está libre.

d) fuerza resultante

Si cualquier fuerza tiene el mismo efecto sobre un cuerpo libre que algún sistema de fuerzas, entonces esta fuerza se llama resultante de este sistema de fuerzas. Esto está escrito de la siguiente manera:

lo que significa equivalencia el impacto sobre el mismo cuerpo libre de la resultante y algún sistema de n fuerzas.

Pasemos ahora a la consideración de conceptos más complejos relacionados con la determinación cuantitativa de los efectos rotacionales de las fuerzas.

e) momento de fuerza relativo a un punto (centro)

Si el cuerpo bajo la acción de una fuerza puede girar alrededor de un punto fijo O (Fig. 2), entonces para cuantificar este efecto de rotación, se introduce una cantidad física, que se llama Momento de fuerza alrededor de un punto (centro).

El plano que pasa por un punto fijo dado y la línea de acción de la fuerza se llama plano de fuerza. En la Fig. 2, este es el plano ОАВ.

El momento de la fuerza relativo a un punto (centro) es una cantidad vectorial igual al producto vectorial del radio vector del punto de aplicación de la fuerza por el vector fuerza:

( 1)

De acuerdo con la regla de la multiplicación vectorial de dos vectores, su producto vectorial es un vector perpendicular al plano de ubicación de los vectores factoriales (en este caso, el plano del triángulo OAB), dirigido en la dirección desde la cual el giro más corto de el vector del primer factor al vector del segundo factor visible contra el reloj (Fig. 2). Con este orden de los vectores de los factores del producto vectorial (1), será visible contrarreloj el giro del cuerpo bajo la acción de la fuerza (Fig. 2) ya que el vector es perpendicular al plano de la fuerza , su ubicación en el espacio determina la posición del plano de la fuerza.. El valor numérico del vector del momento de la fuerza en relación con el centro es igual al doble del área ОАВ y se puede determinar mediante la fórmula:

, (2)

donde magnitudh, igual a la distancia más corta desde un punto O dado hasta la línea de acción de la fuerza, se llama brazo de la fuerza.

Si la posición del plano de acción de la fuerza en el espacio no es esencial para caracterizar la acción de rotación de la fuerza, entonces, en este caso, para caracterizar la acción de rotación de la fuerza, en lugar del vector del momento de la fuerza, momento algebraico de la fuerza:

(3)

El momento algebraico de fuerza relativo a un centro dado es igual al producto del módulo de fuerza y su hombro, tomado con un signo más o menos. En este caso, un momento positivo corresponde a la rotación del cuerpo bajo la acción de una fuerza dada contra el reloj, y un momento negativo corresponde a la rotación del cuerpo en el sentido del reloj. De las fórmulas (1), (2) y (3) se sigue que el momento de la fuerza relativo a un punto es igual a cero solo si el brazo de esta fuerzahcero. Tal fuerza no puede hacer girar el cuerpo alrededor de un punto dado.

f) Momento de fuerza alrededor del eje

Si el cuerpo bajo la acción de una fuerza puede girar alrededor de algún eje fijo (por ejemplo, la rotación del marco de una puerta o ventana en las bisagras cuando se abren o cierran), entonces se introduce una cantidad física para cuantificar este efecto de rotación, que se llama momento de fuerza alrededor de un eje dado.

 B Fxy

La Figura 3 muestra un diagrama según el cual se determina el momento de la fuerza sobre el eje z:

El ángulo  está formado por dos direcciones perpendiculares z y a los planos de los triángulos O abdominales y OAV, respectivamente. Desde  O abdominales es la proyección de ОАВ sobre el plano xy, entonces según el teorema de la estereometría sobre la proyección de una figura plana sobre un plano dado, tenemos:

donde el signo más corresponde a un valor positivo de cos, es decir, ángulos agudos , y el signo menos corresponde a un valor negativo de cos, es decir, ángulos obtusos , debido a la dirección del vector . A su vez, SO abdominales=1/2ah, donde h  abdominales . El valor del segmento abdominales es igual a la proyección de la fuerza sobre el plano xy, es decir . abdominales = F xy .

Con base en lo anterior, así como en las igualdades (4) y (5), determinamos el momento de fuerza con respecto al eje z de la siguiente manera:

La igualdad (6) nos permite formular la siguiente definición del momento de la fuerza con respecto a cualquier eje: El momento de la fuerza con respecto a un eje dado es igual a la proyección sobre este eje del vector del momento de esta fuerza con respecto a cualquier punto de este eje y se define como el producto de la proyección de la fuerza sobre un plano perpendicular al eje dado, tomado con un signo más o menos en el hombro de esta proyección con respecto al punto de intersección del eje con el plano de proyección. En este caso, el signo del momento se considera positivo si, mirando desde la dirección positiva del eje, la rotación del cuerpo alrededor de este eje es visible contrarreloj. De lo contrario, el momento de la fuerza con respecto al eje se toma como negativo. Dado que esta definición del momento de fuerza relativo al eje es bastante difícil de recordar, se recomienda recordar la fórmula (6) y la Fig. 3, que explica esta fórmula.

De la fórmula (6) se sigue que momento de la fuerza con respecto al eje es cero si es paralela al eje (en este caso, su proyección sobre un plano perpendicular al eje es igual a cero), o la línea de acción de la fuerza corta al eje (entonces el brazo de proyección h=0). Esto corresponde completamente al significado físico del momento de la fuerza alrededor del eje como una característica cuantitativa de la acción rotacional de la fuerza sobre un cuerpo con un eje de rotación.

g) peso corporal

Durante mucho tiempo se ha observado que bajo la influencia de una fuerza, el cuerpo adquiere velocidad gradualmente y continúa moviéndose si se elimina la fuerza. Esta propiedad de los cuerpos de resistir un cambio en su movimiento se denominó inercia o inercia de los cuerpos. La medida cuantitativa de la inercia de un cuerpo es su masa. Además, La masa corporal es una medida cuantitativa del efecto de las fuerzas gravitatorias sobre un cuerpo dado. cuanto mayor es la masa del cuerpo, mayor es la fuerza gravitacional que actúa sobre el cuerpo. Como se mostrará a continuación, Oh Estas dos definiciones de peso corporal están relacionadas.

Otros conceptos y definiciones de dinámica se discutirán más adelante en las secciones donde aparecen por primera vez.

2. Enlaces y reacciones de enlaces

Anteriormente en el apartado 1 punto (c) se dio el concepto de cuerpo libre, como un cuerpo que puede moverse en el espacio en cualquier dirección sin estar en contacto directo con otros cuerpos. La mayoría de los cuerpos reales que nos rodean están en contacto directo con otros cuerpos y no pueden moverse en una dirección u otra. Entonces, por ejemplo, los cuerpos ubicados en la superficie de la mesa pueden moverse en cualquier dirección, excepto en la dirección perpendicular a la superficie de la mesa hacia abajo. Las puertas con bisagras pueden girar, pero no pueden moverse hacia adelante, etc. Los cuerpos que no pueden moverse en el espacio en una dirección u otra se llaman no gratuito.

Todo lo que limita el movimiento de un cuerpo dado en el espacio se llama lazos. Estos pueden ser algunos otros cuerpos que impiden el movimiento de este cuerpo en algunas direcciones ( conexiones físicas); más ampliamente, pueden ser algunas condiciones impuestas al movimiento del cuerpo, limitando este movimiento. Entonces, puede poner como condición que el movimiento de un punto material ocurra a lo largo de una curva dada. En este caso, la conexión se especifica matemáticamente en forma de ecuación ( ecuación de conexión). La cuestión de los tipos de enlaces se considerará con más detalle a continuación.

La mayoría de los lazos impuestos a los cuerpos son prácticamente lazos físicos. Por lo tanto, surge la pregunta sobre la interacción de un cuerpo dado y la conexión impuesta a este cuerpo. Esta pregunta se responde con el axioma sobre la interacción de los cuerpos: dos cuerpos actúan uno sobre el otro con fuerzas iguales en magnitud, de dirección opuesta y ubicados en la misma línea recta. Estas fuerzas se denominan fuerzas de interacción. Las fuerzas de interacción se aplican a diferentes cuerpos que interactúan. Entonces, por ejemplo, durante la interacción de un cuerpo dado y una conexión, una de las fuerzas de interacción se aplica desde el lado del cuerpo a la conexión, y la otra fuerza de interacción se aplica desde el lado de la conexión al cuerpo dado. . Esta última potencia se llama fuerza de reacción de enlace o simplemente, reacción de conexión.

Al resolver problemas prácticos de dinámica, es necesario poder encontrar la dirección de las reacciones de varios tipos de enlaces. La regla general para determinar la dirección de una reacción de enlace a veces puede ayudar con esto: la reacción de un enlace siempre se dirige en dirección opuesta a la dirección en la que este enlace impide el movimiento de un cuerpo dado. Si esta dirección se puede especificar definitivamente, entonces la reacción de la conexión estará determinada por la dirección. De lo contrario, la dirección de la reacción del enlace es indefinida y solo se puede encontrar a partir de las correspondientes ecuaciones de movimiento o equilibrio del cuerpo. Con más detalle, la cuestión de los tipos de enlaces y la dirección de sus reacciones debe estudiarse de acuerdo con el libro de texto: S.M. Targ Un curso corto de mecánica teórica "Escuela superior", M., 1986. Capítulo 1, §3.

En la sección 1, punto (c), se dijo que el efecto de cualquier sistema de fuerzas puede determinarse completamente solo si este sistema de fuerzas se aplica a un cuerpo libre. Dado que la mayoría de los cuerpos, de hecho, no son libres, entonces, para estudiar el movimiento de estos cuerpos, surge la pregunta de cómo hacer que estos cuerpos sean libres. esta pregunta esta respondida axioma de conexiones de lecturas en Filosofía en casa. Conferencias fueron... Psicología Social y etnopsicología. 3. Teórico Los resultados en el darwinismo social fueron...

teórico Mecánica

Tutorial >> Física

Resumen conferencias en tema TEÓRICO MECÁNICA Para estudiantes de la especialidad: 260501.65... - jornada completa Resumen conferencias compilado sobre la base de: Butorin L.V., Busygina E.B. teórico Mecánica. Guía didáctica y práctica...

Mecánica teórica- Esta es una rama de la mecánica, que establece las leyes básicas del movimiento mecánico y la interacción mecánica de los cuerpos materiales.

La mecánica teórica es una ciencia en la que se estudian los movimientos de los cuerpos a lo largo del tiempo (movimientos mecánicos). Sirve como base para otras secciones de la mecánica (la teoría de la elasticidad, la resistencia de los materiales, la teoría de la plasticidad, la teoría de los mecanismos y las máquinas, la hidroaerodinámica) y muchas disciplinas técnicas.

movimiento mecanico es cambiar con el tiempo posición mutua en el espacio de los cuerpos materiales.

Interacción mecánica- esta es una interacción de este tipo, como resultado de lo cual cambia el movimiento mecánico o cambia la posición relativa de las partes del cuerpo.

Estática de cuerpo rígido

Estática- Esta es una rama de la mecánica teórica, que se ocupa de los problemas de equilibrio de los cuerpos sólidos y de la transformación de un sistema de fuerzas en otro equivalente a éste.

Conceptos básicos y leyes de la estática.

Cuerpo absolutamente rígido(cuerpo sólido, cuerpo) es un cuerpo material, la distancia entre los puntos en los que no cambia.
punto material es un cuerpo cuyas dimensiones, según las condiciones del problema, pueden despreciarse.
cuerpo suelto es un cuerpo, a cuyo movimiento no se imponen restricciones.
Cuerpo no libre (ligado) Es un cuerpo cuyo movimiento está restringido.
Conexiones- estos son cuerpos que impiden el movimiento del objeto en consideración (un cuerpo o un sistema de cuerpos).
Reacción de comunicación es una fuerza que caracteriza la acción de un enlace sobre un cuerpo rígido. Si consideramos la fuerza con la que un cuerpo rígido actúa sobre un enlace como una acción, entonces la reacción del enlace es una contrarrestación. En este caso, la fuerza - acción se aplica a la conexión y la reacción de la conexión se aplica al cuerpo sólido.
sistema mecánico es un conjunto de cuerpos interconectados o puntos materiales.
Sólido puede considerarse como un sistema mecánico, cuyas posiciones y distancia entre los puntos no cambian.
Fuerza es una cantidad vectorial que caracteriza la acción mecánica de un cuerpo material sobre otro.
La fuerza como vector se caracteriza por el punto de aplicación, la dirección de acción y el valor absoluto. La unidad de medida del módulo de fuerza es Newton.
linea de fuerza es la línea recta a lo largo de la cual se dirige el vector de fuerza.
Poder concentrado es la fuerza aplicada en un punto.
Fuerzas distribuidas (carga distribuida)- son fuerzas que actúan sobre todos los puntos del volumen, superficie o longitud del cuerpo.
La carga distribuida viene dada por la fuerza que actúa por unidad de volumen (superficie, longitud).
La dimensión de la carga distribuida es N / m 3 (N / m 2, N / m).
Fuerza externa es una fuerza que actúa de un cuerpo que no pertenece al sistema mecánico considerado.
fuerza interior es una fuerza que actúa sobre un punto material de un sistema mecánico desde otro punto material perteneciente al sistema considerado.
sistema de fuerza es la totalidad de las fuerzas que actúan sobre un sistema mecánico.
Sistema plano de fuerzas es un sistema de fuerzas cuyas líneas de acción se encuentran en un mismo plano.
Sistema espacial de fuerzas es un sistema de fuerzas cuyas líneas de acción no se encuentran en el mismo plano.
Sistema de fuerzas convergentes Es un sistema de fuerzas cuyas líneas de acción se cortan en un punto.
Sistema arbitrario de fuerzas es un sistema de fuerzas cuyas líneas de acción no se cortan en un punto.
Sistemas de fuerzas equivalentes- estos son sistemas de fuerzas, cuya sustitución una por otra no cambia el estado mecánico del cuerpo.
Designación aceptada: .
Equilibrio Estado en el que un cuerpo permanece estacionario o se mueve uniformemente en línea recta bajo la acción de fuerzas.
sistema equilibrado de fuerzas- este es un sistema de fuerzas que, cuando se aplica a un cuerpo sólido libre, no cambia su estado mecánico (no lo desequilibra).
.
fuerza resultante Es una fuerza cuya acción sobre un cuerpo equivale a la acción de un sistema de fuerzas.
.
Momento de poder es un valor que caracteriza la capacidad de rotación de la fuerza.
pareja de poder Es un sistema de dos fuerzas paralelas iguales en valor absoluto y de dirección opuesta.
Designación aceptada: .
Bajo la acción de un par de fuerzas, el cuerpo realizará un movimiento de rotación.
Proyección de fuerza sobre el eje- este es un segmento encerrado entre perpendiculares dibujadas desde el principio y el final del vector de fuerza a este eje.
La proyección es positiva si la dirección del segmento coincide con la dirección positiva del eje.
Proyección de fuerza en un plano es un vector en un plano encerrado entre las perpendiculares trazadas desde el principio y el final del vector fuerza a este plano.
Ley 1 (ley de la inercia). Un punto material aislado está en reposo o se mueve uniforme y rectilíneamente.
El movimiento uniforme y rectilíneo de un punto material es un movimiento por inercia. El estado de equilibrio de un punto material y un cuerpo rígido se entiende no sólo como un estado de reposo, sino también como un movimiento por inercia. Para un cuerpo rígido, hay diferentes tipos movimiento por inercia, por ejemplo, la rotación uniforme de un cuerpo rígido alrededor de un eje fijo.
Ley 2. Un cuerpo rígido está en equilibrio bajo la acción de dos fuerzas solo si estas fuerzas son de igual magnitud y están dirigidas en direcciones opuestas a lo largo de una línea de acción común.
Estas dos fuerzas se llaman equilibradas.
En general, se dice que las fuerzas están equilibradas si el cuerpo rígido al que se aplican estas fuerzas está en reposo.
Ley 3. Sin violar el estado (la palabra "estado" aquí significa el estado de movimiento o reposo) de un cuerpo rígido, uno puede agregar y descartar fuerzas de equilibrio.
Consecuencia. Sin alterar el estado de un cuerpo rígido, la fuerza se puede transferir a lo largo de su línea de acción a cualquier punto del cuerpo.
Dos sistemas de fuerzas se llaman equivalentes si uno de ellos puede ser reemplazado por otro sin alterar el estado del cuerpo rígido.
Ley 4. La resultante de dos fuerzas aplicadas en un punto se aplica en el mismo punto, es igual en valor absoluto a la diagonal del paralelogramo construido sobre estas fuerzas y está dirigida a lo largo de este
diagonales
El módulo de la resultante es:
Ley 5 (ley de igualdad de acción y reacción). Las fuerzas con las que actúan dos cuerpos entre sí son de igual magnitud y están dirigidas en direcciones opuestas a lo largo de una línea recta.
Debe tenerse en cuenta que acción- fuerza aplicada al cuerpo B, Y oposición- fuerza aplicada al cuerpo PERO, no están equilibrados, ya que están unidos a cuerpos diferentes.
Ley 6 (la ley del endurecimiento). El equilibrio de un cuerpo no sólido no se altera cuando se solidifica.
No debe olvidarse que las condiciones de equilibrio, que son necesarias y suficientes para un cuerpo rígido, son necesarias pero insuficientes para el correspondiente cuerpo no rígido.
Ley 7 (la ley de liberación de bonos). Un sólido no libre puede considerarse libre si se libera mentalmente de los enlaces, reemplazando la acción de los enlaces con las correspondientes reacciones de los enlaces.

Conexiones y sus reacciones.

Superficie lisa restringe el movimiento a lo largo de la normal a la superficie de apoyo. La reacción se dirige perpendicularmente a la superficie.
Soporte móvil articulado limita el movimiento del cuerpo a lo largo de la normal al plano de referencia. La reacción se dirige a lo largo de la normal a la superficie de apoyo.
Soporte fijo articulado contrarresta cualquier movimiento en un plano perpendicular al eje de rotación.
Caña ingrávida articulada contrarresta el movimiento del cuerpo a lo largo de la línea de la varilla. La reacción se dirigirá a lo largo de la línea de la barra.
terminación ciega contrarresta cualquier movimiento y rotación en el plano. Su acción puede ser sustituida por una fuerza presentada en forma de dos componentes y un par de fuerzas con un momento.

Cinemática

Cinemática- una rama de la mecánica teórica que se ocupa de general propiedades geométricas movimiento mecánico como un proceso que ocurre en el espacio y el tiempo. Los objetos en movimiento se consideran puntos geométricos o cuerpos geométricos.

Conceptos básicos de cinemática.

La ley de movimiento de un punto (cuerpo) es la dependencia de la posición de un punto (cuerpo) en el espacio con respecto al tiempo.
Punto de trayectoria es el lugar geométrico de las posiciones de un punto en el espacio durante su movimiento.
Velocidad del punto (cuerpo)- esta es una característica del cambio en el tiempo de la posición de un punto (cuerpo) en el espacio.
Aceleración puntual (cuerpo)- esta es una característica del cambio en el tiempo de la velocidad de un punto (cuerpo).

Determinación de las características cinemáticas de un punto

Punto de trayectoria
En el sistema de referencia vectorial, la trayectoria se describe mediante la expresión: .
En el sistema de coordenadas de referencia, la trayectoria se determina según la ley del movimiento puntual y se describe mediante las expresiones z = f(x,y) en el espacio, o y = f(x)- en el avión.
En un sistema de referencia natural, la trayectoria está predeterminada.
Determinación de la velocidad de un punto en un sistema de coordenadas vectoriales
Al especificar el movimiento de un punto en un sistema de coordenadas vectoriales, la relación entre el movimiento y el intervalo de tiempo se denomina valor promedio de la velocidad en este intervalo de tiempo: .
Tomando el intervalo de tiempo como un valor infinitesimal, se obtiene el valor de la velocidad en un momento dado (el valor instantáneo de la velocidad): .
El vector de velocidad promedio se dirige a lo largo del vector en la dirección del movimiento del punto, el vector de velocidad instantánea se dirige tangencialmente a la trayectoria en la dirección del movimiento del punto.
Producción: la velocidad de un punto es una cantidad vectorial igual a la derivada de la ley del movimiento con respecto al tiempo.
Propiedad derivada: la derivada temporal de cualquier valor determina la tasa de cambio de este valor.
Determinación de la velocidad de un punto en un sistema de referencia de coordenadas
Tasa de cambio de las coordenadas del punto:
.
El módulo de la velocidad total de un punto con sistema de coordenadas rectangular será igual a:
.
La dirección del vector de velocidad está determinada por los cosenos de los ángulos de dirección:
,
donde son los ángulos entre el vector velocidad y los ejes de coordenadas.
Determinación de la velocidad de un punto en un sistema de referencia natural
La velocidad de un punto en un sistema de referencia natural se define como una derivada de la ley de movimiento de un punto: .
De acuerdo con las conclusiones anteriores, el vector velocidad está dirigido tangencialmente a la trayectoria en la dirección del movimiento del punto y en los ejes está determinado por una sola proyección.

Cinemática de cuerpo rígido

En la cinemática de cuerpos rígidos se resuelven dos problemas principales:
1) tarea de movimiento y determinación de las características cinemáticas del cuerpo en su conjunto;
2) determinación de las características cinemáticas de los puntos del cuerpo.
Movimiento de traslación de un cuerpo rígido.
El movimiento de traslación es un movimiento en el que una línea recta trazada a través de dos puntos del cuerpo permanece paralela a su posición original.
Teorema: En el movimiento de traslación, todos los puntos del cuerpo se mueven a lo largo de las mismas trayectorias y en cada momento tienen las mismas velocidades y aceleraciones en magnitud y dirección..
Producción: el movimiento de traslación de un cuerpo rígido está determinado por el movimiento de cualquiera de sus puntos, y por lo tanto, la tarea y estudio de su movimiento se reduce a la cinemática de un punto.
Movimiento de rotación de un cuerpo rígido alrededor de un eje fijo
El movimiento de rotación de un cuerpo rígido alrededor de un eje fijo es el movimiento de un cuerpo rígido en el que dos puntos pertenecientes al cuerpo permanecen inmóviles durante todo el tiempo del movimiento.
La posición del cuerpo está determinada por el ángulo de rotación. La unidad de medida de un ángulo son los radianes. (Un radián es el ángulo central de un círculo cuya longitud de arco es igual al radio, el ángulo completo del círculo contiene 2π radián.)
La ley del movimiento de rotación de un cuerpo alrededor de un eje fijo.
La velocidad angular y la aceleración angular del cuerpo se determinarán por el método de diferenciación:
— velocidad angular, rad/s;
— aceleración angular, rad/s².
Si cortamos el cuerpo por un plano perpendicular al eje, elegimos un punto en el eje de rotación DESDE y un punto arbitrario METRO, entonces el punto METRO describirá alrededor del punto DESDE círculo de radio R. Durante dt hay una rotación elemental a través del ángulo , mientras que el punto METRO se moverá a lo largo de la trayectoria por una distancia .
Módulo de velocidad lineal:
.
punto de aceleración METRO con una trayectoria conocida está determinada por sus componentes:
,
donde .
Como resultado, obtenemos fórmulas
aceleración tangencial: ;
aceleración normal: .

Dinámica

Dinámica- Es una rama de la mecánica teórica, que estudia los movimientos mecánicos de los cuerpos materiales, en función de las causas que los provocan.

Conceptos básicos de dinámica.

inercia- esta es la propiedad de los cuerpos materiales para mantener un estado de reposo o movimiento rectilíneo uniforme hasta que fuerzas externas cambien este estado.
Peso es una medida cuantitativa de la inercia de un cuerpo. La unidad de masa es el kilogramo (kg).
punto material es un cuerpo con una masa, cuyas dimensiones se desprecian al resolver este problema.
Centro de masa de un sistema mecánico. es un punto geométrico cuyas coordenadas están determinadas por las fórmulas:

donde metro k , x k , y k , z k- masa y coordenadas k- ese punto del sistema mecánico, metro es la masa del sistema.
En un campo de gravedad uniforme, la posición del centro de masa coincide con la posición del centro de gravedad.
Momento de inercia de un cuerpo material sobre el eje es una medida cuantitativa de la inercia durante el movimiento de rotación.
El momento de inercia de un punto material respecto al eje es igual al producto de la masa del punto por el cuadrado de la distancia del punto al eje:
.
El momento de inercia del sistema (cuerpo) con respecto al eje es igual a la suma aritmética de los momentos de inercia de todos los puntos:
La fuerza de inercia de un punto material. es una cantidad vectorial igual en valor absoluto al producto de la masa de un punto y el módulo de aceleración y en dirección opuesta al vector aceleración:
Fuerza de inercia de un cuerpo material. es una cantidad vectorial igual en valor absoluto al producto de la masa del cuerpo y el módulo de aceleración del centro de masa del cuerpo y en dirección opuesta al vector de aceleración del centro de masa: ,
donde es la aceleración del centro de masa del cuerpo.
Impulso de fuerza elemental es una cantidad vectorial igual al producto del vector fuerza por un intervalo de tiempo infinitesimal dt:
.
El impulso total de fuerza para Δt es igual a la integral de impulsos elementales:
.
trabajo de fuerza elemental es un escalar dA, igual al escalar

institución autónoma del estado

Región de Kaliningrado

profesional organización educativa

Facultad de Servicio y Turismo

Curso de conferencias con ejemplos. tareas practicas

"Fundamentos de Mecánica Teórica"

por disciplinamecanica tecnica

para estudiantes3 curso

especialidad20.02.04 Seguridad contra incendios

Kaliningrado

APROBAR

Director Adjunto de SD GAU KO VEO KSTN.N. Miasnikov

APROBADO

Consejo Metodológico de GAU KO VET KST

CONSIDERADO

En una reunión del PCC

Equipo editorial:

Kolganova A.A., metodóloga

Falaleeva A.B., profesora de lengua y literatura rusas

Tsvetaeva L.V., presidenta del PCCdisciplinas generales de matemáticas y ciencias naturales

Compilado por:

Nezvanova I.V. Profesor GAU KO VET KST

Contenido

Dinámica: conceptos básicos y axiomas

Bibliografía

Estática: conceptos básicos y axiomas.

Información teórica

Estática - una sección de mecánica teórica, que considera las propiedades de las fuerzas aplicadas a los puntos de un cuerpo rígido, y las condiciones para su equilibrio. Tareas principales:

1. Transformación de sistemas de fuerzas en sistemas de fuerzas equivalentes.

2. Determinación de las condiciones de equilibrio de sistemas de fuerzas que actúan sobre un cuerpo rígido.

punto material llamado el modelo más simple de un cuerpo material

cualquier forma, cuyas dimensiones sean lo suficientemente pequeñas y que puedan tomarse como punto geométrico tener cierta masa. Un sistema mecánico es cualquier conjunto de puntos materiales. Un cuerpo absolutamente rígido es un sistema mecánico, cuyas distancias entre los puntos no cambian bajo ninguna interacción.

Fuerza es una medida de la interacción mecánica de los cuerpos materiales entre sí. La fuerza es una cantidad vectorial, ya que está determinada por tres elementos:

valor numérico;

dirección;

punto de aplicación (A).

La unidad de fuerza es Newton (N).

Figura 1.1

Un sistema de fuerzas es un conjunto de fuerzas que actúan sobre un cuerpo.

Un sistema de fuerzas equilibrado (igual a cero) es un sistema que, aplicado a un cuerpo, no cambia su estado.

El sistema de fuerzas que actúa sobre el cuerpo puede ser reemplazado por una resultante que actúa como sistema de fuerzas.

Axiomas de la estática.

Axioma 1: Si se aplica un sistema equilibrado de fuerzas al cuerpo, entonces se mueve de manera uniforme y rectilínea o está en reposo (la ley de la inercia).

Axioma 2: Un cuerpo absolutamente rígido está en equilibrio bajo la acción de dos fuerzas si y solo si estas fuerzas son iguales en valor absoluto, actúan en una línea recta y están dirigidas en direcciones opuestas. Figura 1.2

Axioma 3: El estado mecánico del cuerpo no se alterará si al sistema de fuerzas que actúan sobre él se le suma o se le resta un sistema equilibrado de fuerzas.

Axioma 4: La resultante de las dos fuerzas aplicadas al cuerpo es igual a su suma geométrica, es decir, se expresa en valor absoluto y dirección por la diagonal del paralelogramo construido sobre estas fuerzas como sobre los lados.

Figura 1.3.

Axioma 5: Las fuerzas con las que actúan dos cuerpos entre sí son siempre iguales en valor absoluto y dirigidas a lo largo de una línea recta en direcciones opuestas.

Figura 1.4.

Tipos de enlaces y sus reacciones.

conexiones Se denominan restricciones a todas las que impiden el movimiento del cuerpo en el espacio. El cuerpo, buscando bajo la acción de las fuerzas aplicadas moverse, lo cual es impedido por la unión, actuará sobre él con una cierta fuerza llamada fuerza de presión sobre la conexión . De acuerdo con la ley de igualdad de acción y reacción, la conexión actuará sobre el cuerpo con el mismo módulo, pero con una fuerza de dirección opuesta.
La fuerza con la que esta conexión actúa sobre el cuerpo, impidiendo uno u otro movimiento, se llama la fuerza de reacción (reacción) del enlace .
Uno de los principios fundamentales de la mecánica es principio de liberación : cualquier cuerpo no libre puede considerarse libre, si descartamos los enlaces y reemplazamos su acción con las reacciones de los enlaces.

La reacción de enlace se dirige en la dirección opuesta a donde el enlace no permite que el cuerpo se mueva. Los principales tipos de enlaces y sus reacciones se muestran en la Tabla 1.1.

Tabla 1.1

Tipos de enlaces y sus reacciones.

Nombre de la comunicación

Símbolo

Superficie lisa (soporte) - la superficie (soporte), la fricción en la que se puede despreciar el cuerpo dado.
Con apoyo gratuito, la reacciónestá dirigida perpendicularmente a la tangente que pasa por el puntoPERO contacto corporal1 con superficie de apoyo2 .

Hilo (flexible, inextensible). La conexión, realizada en forma de hilo inextensible, no permite que el cuerpo se aleje del punto de suspensión. Por tanto, la reacción del hilo se dirige a lo largo del hilo hasta el punto de su suspensión.

varilla sin peso – una barra, cuyo peso puede despreciarse en comparación con la carga percibida.
La reacción de una barra rectilínea articulada sin peso se dirige a lo largo del eje de la barra.

Bisagra móvil, soporte móvil articulado. La reacción se dirige a lo largo de la normal a la superficie de apoyo.

Cierre rígido. En el plano del empotramiento rígido habrá dos componentes de la reacción, y momento de un par de fuerzas, que evita que el haz gire1 relativo al puntoPERO .
Una unión rígida en el espacio le quita los seis grados de libertad al cuerpo 1: tres desplazamientos a lo largo de los ejes de coordenadas y tres rotaciones alrededor de estos ejes.
Habrá tres componentes en el empotramiento rígido espacial, , y tres momentos de pares de fuerzas.

Sistema de fuerzas convergentes

Un sistema de fuerzas convergentes. Se denomina sistema de fuerzas cuyas líneas de acción se cortan en un punto. Dos fuerzas que convergen en un punto, de acuerdo con el tercer axioma de la estática, pueden ser reemplazadas por una fuerza:resultante .
El vector principal del sistema de fuerzas. - un valor igual a la suma geométrica de las fuerzas del sistema.

La resultante de un sistema plano de fuerzas convergentes Puede ser definidográficamente Y analíticamente.

Adición de un sistema de fuerzas. . La suma de un sistema plano de fuerzas convergentes se realiza ya sea mediante la suma sucesiva de fuerzas con la construcción de una resultante intermedia (figura 1.5), o mediante la construcción de un polígono de fuerzas (figura 1.6).

Figura 1.5Figura 1.6

Proyección de fuerza sobre el eje - una cantidad algebraica igual al producto del módulo de fuerza y el coseno del ángulo entre la fuerza y la dirección positiva del eje.
ProyecciónFX(fig.1.7) fuerzas por eje Xpositivo si α es agudo, negativo si α es obtuso. si la fuerzaes perpendicular al eje, entonces su proyección sobre el eje es cero.

Figura 1.7

Proyección de fuerza en un plano Ohu- vectores , concluido entre las proyecciones del inicio y final de la fuerzaa este avión. Esos. la proyección de la fuerza sobre el plano es una cantidad vectorial, caracterizada no sólo valor numérico, sino también la dirección en el planoOhu (Figura 1.8).

Figura 1.8

Entonces el módulo de proyección al avión Ohu será igual a:

Fxy = F porque,

donde α es el ángulo entre la dirección de la fuerza y su proyección.
Manera analítica de especificar fuerzas. . Para el método analítico de ajuste de la fuerzaes necesario elegir un sistema de ejes de coordenadasOhz, en relación con la cual se determinará la dirección de la fuerza en el espacio.
Un vector que representa la fuerza., se puede construir si se conocen el módulo de esta fuerza y los ángulos α, β, γ que forma la fuerza con los ejes de coordenadas. PuntoPERO aplicación de la fuerza fijado por separado por sus coordenadasX, en, z. Puedes establecer la fuerza por sus proyecciones.efectos especiales, fy, fzen los ejes de coordenadas. El módulo de fuerza en este caso está determinado por la fórmula:

y cosenos directores:

, .

Método analítico de suma de fuerzas. : la proyección del vector suma sobre algún eje es igual a la suma algebraica de las proyecciones de los términos de los vectores sobre el mismo eje, es decir, si:

luego , , .
Conocimiento Rx, Ry, Rz, podemos definir el módulo

y cosenos directores:

, , .

Figura 1.9

Para el equilibrio de un sistema de fuerzas convergentes, es necesario y suficiente que la resultante de estas fuerzas sea igual a cero.
1) Condición de equilibrio geométrico para un sistema de fuerzas convergentes : para el equilibrio de un sistema de fuerzas convergentes, es necesario y suficiente que el polígono de fuerzas construido a partir de estas fuerzas

fue cerrado (el final del vector del último término

fuerza debe coincidir con el comienzo del vector del primer término de la fuerza). Entonces el vector principal del sistema de fuerzas será igual a cero ()
2) Condiciones de equilibrio analítico . El módulo del vector principal del sistema de fuerzas está determinado por la fórmula. =0. En la medida en , entonces la expresión raíz puede ser igual a cero solo si cada término desaparece simultáneamente, es decir

Rx= 0, Ry= 0, R z = 0.

Por tanto, para el equilibrio del sistema espacial de fuerzas convergentes, es necesario y suficiente que las sumas de las proyecciones de estas fuerzas sobre cada una de las tres coordenadas de los ejes sean iguales a cero:

Para el equilibrio de un sistema plano de fuerzas convergentes, es necesario y suficiente que la suma de las proyecciones de fuerzas en cada uno de los dos ejes de coordenadas sea igual a cero:

Suma de dos fuerzas paralelas en la misma dirección.

Figura 1.9

Dos fuerzas paralelas dirigidas en la misma dirección se reducen a una fuerza resultante paralela a ellas y dirigida en la misma dirección. La magnitud de la resultante es igual a la suma de las magnitudes de estas fuerzas, y el punto de su aplicación C divide internamente la distancia entre las líneas de acción de las fuerzas en partes inversamente proporcionales a las magnitudes de estas fuerzas, es decir

BAC

R=F 1 +F 2

La suma de dos fuerzas paralelas desiguales dirigidas en direcciones opuestas.

Dos fuerzas antiparalelas desiguales se reducen a una fuerza resultante paralela a ellas y dirigida hacia la fuerza mayor. La magnitud de la resultante es igual a la diferencia entre las magnitudes de estas fuerzas, y el punto de su aplicación, C, divide la distancia entre las líneas de acción de las fuerzas externas en partes inversamente proporcionales a las magnitudes de estas fuerzas, que es

Par de fuerzas y momento de fuerza respecto a un punto.

Momento de fuerza con respecto al punto O se llama, tomado con el signo apropiado, el producto de la magnitud de la fuerza por la distancia h desde el punto O hasta la línea de acción de la fuerza . Este producto se toma con un signo más si la fuerza tiende a girar el cuerpo en sentido antihorario, y con el signo -, si la fuerza tiende a girar el cuerpo en el sentido de las agujas del reloj, es decir . La longitud de la perpendicular h se llamahombro de fuerza punto O. El efecto de la acción de la fuerza, es decir. la aceleración angular del cuerpo es mayor cuanto mayor es la magnitud del momento de la fuerza.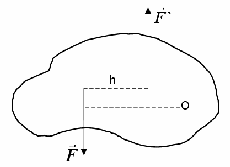

Figura 1.11

un par de fuerzas Se denomina sistema a un sistema formado por dos fuerzas paralelas de igual magnitud, dirigidas en direcciones opuestas. La distancia h entre las líneas de acción de las fuerzas se llamaparejas de hombros . Momento de un par de fuerzas m(F,F") es el producto del valor de una de las fuerzas que forman el par y el brazo del par, tomado con el signo correspondiente.

Se escribe como sigue: m(F, F")= ± F × h, donde el producto se toma con signo más si el par de fuerzas tiende a girar el cuerpo en sentido antihorario y con signo menos si el par de fuerzas tiende para girar el cuerpo en el sentido de las agujas del reloj.

El teorema de la suma de los momentos de fuerzas de un par.

La suma de los momentos de fuerzas del par (F,F") con respecto a cualquier punto 0 tomado en el plano de acción del par no depende de la elección de este punto y es igual al momento del par.

Teorema de los pares equivalentes. Consecuencias.

Teorema. Dos pares cuyos momentos son iguales entre sí son equivalentes, es decir (F, F") ~ (P, P")

Corolario 1 . Un par de fuerzas se puede transferir a cualquier lugar en el plano de su acción, así como rotar a cualquier ángulo y cambiar el brazo y la magnitud de las fuerzas del par, mientras se mantiene el momento del par.

consecuencia 2. Un par de fuerzas no tiene resultante y no puede equilibrarse con una fuerza que se encuentre en el plano del par.

Figura 1.12

Adición y condición de equilibrio para un sistema de pares en un plano.

1. Teorema de la suma de pares que se encuentran en el mismo plano. Un sistema de pares, ubicado arbitrariamente en el mismo plano, puede ser reemplazado por un par, cuyo momento es igual a la suma de los momentos de estos pares.

2. Teorema sobre el equilibrio de un sistema de pares en un plano.

Para que un cuerpo absolutamente rígido esté en reposo bajo la acción de un sistema de pares, arbitrariamente ubicados en el mismo plano, es necesario y suficiente que la suma de los momentos de todos los pares sea igual a cero, es decir

Centro de gravedad

la fuerza de la gravedad - la resultante de las fuerzas de atracción de la Tierra, distribuidas en todo el volumen del cuerpo.

Centro de gravedad del cuerpo - este es un punto, invariablemente asociado con este cuerpo, a través del cual pasa la línea de acción de la fuerza de gravedad de un cuerpo dado en cualquier posición del cuerpo en el espacio.

Métodos para encontrar el centro de gravedad.

1. Método de simetría:

1.1. Si un cuerpo homogéneo tiene un plano de simetría, entonces el centro de gravedad se encuentra en este plano

1.2. Si un cuerpo homogéneo tiene un eje de simetría, entonces el centro de gravedad se encuentra en este eje. El centro de gravedad de un cuerpo de revolución homogéneo se encuentra sobre el eje de revolución.

1.3 Si un cuerpo homogéneo tiene dos ejes de simetría, entonces el centro de gravedad está en el punto de su intersección.

2. Método de partición: el cuerpo se divide en el menor número de partes, cuyas fuerzas de gravedad y la posición de los centros de gravedad se conocen.

3. Método de masas negativas: Al determinar el centro de gravedad de un cuerpo con cavidades libres, se debe utilizar el método de partición, pero la masa de cavidades libres debe considerarse negativa.

Coordenadas del centro de gravedad de una figura plana:

Las posiciones de los centros de gravedad de simples formas geométricas puede calcularse usando fórmulas conocidas. (Figura 1.13)

Nota: El centro de gravedad de la simetría de la figura está en el eje de simetría.

El centro de gravedad de la varilla está en el medio de la altura.

1.2. Ejemplos de resolución de problemas prácticos.

Ejemplo 1: Un peso está suspendido de una barra y está en equilibrio. Determine las fuerzas en la barra. (Figura 1.2.1)

Solución:

Las fuerzas que surgen en las varillas de sujeción son iguales en magnitud a las fuerzas con las que las varillas soportan la carga. (quinto axioma)

Determinamos las posibles direcciones de las reacciones de los enlaces "varillas rígidas".

Los esfuerzos se dirigen a lo largo de las varillas.

Figura 1.2.1.

Liberemos el punto A de los enlaces, reemplazando la acción de los enlaces con sus reacciones. (Figura 1.2.2)

Comencemos la construcción con una fuerza conocida dibujando un vectorFen alguna escala.

Desde el final del vectorFdibujar líneas paralelas a las reaccionesR 1 YR 2 .

Figura 1.2.2

Al intersecarse, las líneas crean un triángulo. (Figura 1.2.3.). Conociendo la escala de las construcciones y midiendo la longitud de los lados del triángulo, es posible determinar la magnitud de las reacciones en las varillas.

Para cálculos más precisos, puede usar relaciones geométricas, en particular, el teorema del seno: la relación entre el lado del triángulo y el seno del ángulo opuesto es un valor constante

Para este caso:

Figura 1.2.3

Comentario: Si la dirección del vector (reacción de acoplamiento) en un esquema dado y en el triángulo de fuerzas no coincidieron, entonces la reacción en el esquema debe dirigirse en la dirección opuesta.

Ejemplo 2: Determine la magnitud y la dirección del sistema plano resultante de fuerzas convergentes de forma analítica.

Solución:

Figura 1.2.4

1. Determinamos las proyecciones de todas las fuerzas del sistema sobre Ox (Figura 1.2.4)

Sumando algebraicamente las proyecciones, obtenemos la proyección de la resultante sobre el eje Ox.

El signo indica que la resultante se dirige hacia la izquierda.

2. Determinamos las proyecciones de todas las fuerzas sobre el eje Oy:

Sumando algebraicamente las proyecciones, obtenemos la proyección de la resultante sobre el eje Oy.

El signo indica que la resultante se dirige hacia abajo.

3. Determinar el módulo de la resultante por las magnitudes de las proyecciones:

4. Determinar el valor del ángulo de la resultante con el eje Ox:

y el valor del ángulo con el eje y:

Ejemplo 3: Calcular la suma de los momentos de las fuerzas relativas al punto O (Figura 1.2.6).

OA= AB= END=DE=CB=2metro

Figura 1.2.6

Solución:

1. El momento de la fuerza relativo a un punto es numéricamente igual al producto del módulo y el brazo de la fuerza.

2. El momento de la fuerza es igual a cero si la línea de acción de la fuerza pasa por un punto.

Ejemplo 4: Determine la posición del centro de gravedad de la figura que se muestra en la Figura 1.2.7

Solución:

Descomponemos la figura en tres:

1-rectángulo

PERO 1 =10*20=200cm 2

2-triángulo

PERO 2 =1/2*10*15=75cm 2

3 vueltas

PERO 3 =3,14*3 2 = 28,3 cm 2

Figura 1 GC: x 1 = 10 cm, y 1 = 5cm

Figura 2 GC: x 2 =20+1/3*15=25cm, tu 2 =1/3*10=3,3 cm

Figura 3 GC: x 3 = 10 cm, y 3 = 5cm

Se define de manera similar para desde = 4,5 cm

Cinemática: conceptos básicos.

Parámetros cinemáticos básicos

Trayectoria - la línea que traza un punto material al moverse en el espacio. La trayectoria puede ser una línea recta y una curva, un plano y una línea espacial.

Ecuación de trayectoria para movimiento plano: y =F ( X)

Distancia viajada. La trayectoria se mide a lo largo de la trayectoria en la dirección de desplazamiento. Designacion -S, unidades de medida - metros.

Ecuación de movimiento puntual es una ecuación que determina la posición de un punto en movimiento en función del tiempo.

Figura 2.1

La posición de un punto en cada momento del tiempo puede determinarse por la distancia recorrida a lo largo de la trayectoria desde algún punto fijo, considerado como el origen (Figura 2.1). Este tipo de movimiento se llamanatural . Por lo tanto, la ecuación de movimiento se puede representar como S = f (t).

Figura 2.2

La posición de un punto también se puede determinar si se conocen sus coordenadas en función del tiempo (Figura 2.2). Entonces, en el caso de movimiento en un plano, se deben dar dos ecuaciones:

Cuándo movimiento espacial se suma la tercera coordenadaz= F 3 ( t)

Este tipo de movimiento se llamacoordinar .

Velocidad de viaje es una cantidad vectorial que caracteriza en el momento la velocidad y la dirección del movimiento a lo largo de la trayectoria.

La velocidad es un vector dirigido en cualquier momento tangencialmente a la trayectoria hacia la dirección del movimiento (Figura 2.3).

Figura 2.3

Si un punto recorre distancias iguales en intervalos de tiempo iguales, entonces el movimiento se llamauniforme .

velocidad media en el camino ΔSdefinido:

donde∆S- distancia recorrida en el tiempo Δt; Δ t- intervalo de tiempo.

Si un punto recorre trayectorias desiguales en intervalos de tiempo iguales, entonces el movimiento se llamadesigual . En este caso, la velocidad es una variable y depende del tiempo.v= F( t)

La velocidad actual se define como

punto de aceleración - una cantidad vectorial que caracteriza la tasa de cambio de velocidad en magnitud y dirección.

La velocidad de un punto cuando se mueve del punto M1 al punto Mg cambia en magnitud y dirección. El valor promedio de la aceleración para este período de tiempo

Aceleración actual:

Usualmente, por conveniencia, se consideran dos componentes de aceleración mutuamente perpendiculares: normal y tangencial (Figura 2.4)

Aceleración normal a norte , caracteriza el cambio de velocidad por

dirección y se define como

La aceleración normal siempre se dirige perpendicularmente a la velocidad hacia el centro del arco.

Figura 2.4

Aceleración tangencial a t , caracteriza el cambio de velocidad en magnitud y siempre se dirige tangencialmente a la trayectoria; durante la aceleración, su dirección coincide con la dirección de la velocidad, y durante la desaceleración, su dirección es opuesta a la dirección del vector velocidad.

El valor de aceleración total se define como:

Análisis de tipos y parámetros cinemáticos de movimientos.

movimiento uniforme - Este es un movimiento a velocidad constante:

Para movimiento uniforme rectilíneo:

Para movimiento curvilíneo uniforme:

Ley del movimiento uniforme :

Movimiento de igual variable – es un movimiento con aceleración tangencial constante:

Para movimiento uniforme rectilíneo

Para movimiento curvilíneo uniforme:

Ley del movimiento uniforme:

Gráficos cinemáticos

Gráficos cinemáticos - Son gráficas de cambios de trayectoria, velocidad y aceleración en función del tiempo.

Movimiento uniforme (Figura 2.5)

Figura 2.5

Movimiento de igual variable (figura 2.6)

Figura 2.6

Los movimientos más simples de un cuerpo rígido.

Movimiento hacia adelante llamado movimiento de un cuerpo rígido, en el cual cualquier línea recta sobre el cuerpo durante el movimiento permanece paralela a su posición inicial (Figura 2.7)

Figura 2.7

En el movimiento de traslación, todos los puntos del cuerpo se mueven de la misma manera: las velocidades y aceleraciones son las mismas en todo momento.

Enmovimiento rotatorio todos los puntos del cuerpo describen círculos alrededor de un eje fijo común.

El eje fijo alrededor del cual giran todos los puntos del cuerpo se llamaeje de rotación.

Para describir el movimiento de rotación de un cuerpo alrededor de un eje fijo, sóloopciones de esquina (Figura 2.8)

φ es el ángulo de rotación del cuerpo;

ω – velocidad angular, determina el cambio en el ángulo de rotación por unidad de tiempo;

El cambio en la velocidad angular con el tiempo se determina aceleración angular:

2.2. Ejemplos de resolución de problemas prácticos.

Ejemplo 1: Se da la ecuación de movimiento de un punto. Determine la velocidad del punto al final del tercer segundo de movimiento y la velocidad promedio de los primeros tres segundos.

Solución:

1. Ecuación de la velocidad

2. Velocidad al final del tercer segundo (t=3 C)

3. Velocidad media

Ejemplo 2: De acuerdo con la ley de movimiento dada, determine el tipo de movimiento, la velocidad inicial y la aceleración tangencial del punto, el tiempo para detenerse.

Solución:

1. Tipo de movimiento: igualmente variable ()
2. Al comparar las ecuaciones, es obvio que

- el camino inicial recorrido antes del inicio de la cuenta regresiva 10m;

- velocidad inicial 20m/s

- aceleración tangencial constante

- la aceleración es negativa, por lo tanto, el movimiento es lento, la aceleración se dirige en la dirección opuesta a la velocidad del movimiento.

3. Puedes determinar el tiempo en el que la velocidad del punto será igual a cero.

3. Dinámica: conceptos básicos y axiomas

Dinámica - una sección de mecánica teórica en la que se establece una conexión entre el movimiento de los cuerpos y las fuerzas que actúan sobre ellos.

En dinámica se resuelven dos tipos de problemas:

determinar los parámetros de movimiento de acuerdo con las fuerzas dadas;

determinar las fuerzas que actúan sobre el cuerpo, de acuerdo con los parámetros cinemáticos de movimiento dados.

Bajopunto material implican cierto cuerpo que tiene cierta masa (es decir, contiene cierta cantidad de materia), pero no tiene dimensiones lineales (un volumen de espacio infinitesimal).
aislado se considera un punto material, que no se ve afectado por otros puntos materiales. EN mundo real no existen puntos materiales aislados, así como cuerpos aislados, este concepto es condicional.

Con el movimiento de traslación, todos los puntos del cuerpo se mueven de la misma manera, por lo que el cuerpo puede tomarse como un punto material.

Si las dimensiones del cuerpo son pequeñas en comparación con la trayectoria, también se puede considerar como un punto material, mientras que el punto coincide con el centro de gravedad del cuerpo.

Durante el movimiento de rotación del cuerpo, los puntos pueden no moverse de la misma manera, en este caso, algunas disposiciones de la dinámica pueden aplicarse solo a puntos individuales, y el objeto material puede considerarse como un conjunto de puntos materiales.

Por lo tanto, la dinámica se divide en la dinámica de un punto y la dinámica de un sistema material.

Axiomas de la dinámica

Primer axioma ( principio de inercia): en todo punto material aislado se encuentra en estado de reposo o de movimiento uniforme y rectilíneo hasta que las fuerzas aplicadas lo sacan de ese estado.

Este estado se llama estadoinercia. Retire el punto de este estado, es decir, darle algo de aceleración, tal vez una fuerza externa.

Todo cuerpo (punto) tieneinercia. La medida de la inercia es la masa del cuerpo.

Masa llamadola cantidad de materia en un cuerpo en la mecánica clásica, se considera una constante. La unidad de masa es el kilogramo (kg).

Segundo axioma (La segunda ley de Newton es la ley básica de la dinámica)

F = ma

dondeT - masa puntual, kg;pero - punto de aceleración, m/s 2 .

La aceleración impartida a un punto material por una fuerza es proporcional a la magnitud de la fuerza y coincide con la dirección de la fuerza.

La gravedad actúa sobre todos los cuerpos de la Tierra, imparte al cuerpo la aceleración de caída libre, dirigida hacia el centro de la Tierra:

G=mg

dondegramo- 9,81 m/s², aceleración de caída libre.

Tercer axioma (Tercera ley de Newton): conLas fuerzas de interacción de dos cuerpos son de igual magnitud y están dirigidas a lo largo de la misma línea recta en diferentes direcciones.

Al interactuar, las aceleraciones son inversamente proporcionales a las masas.

Cuarto axioma (ley de independencia de acción de las fuerzas): aCada fuerza del sistema de fuerzas actúa como actuaría sola.

La aceleración impartida al punto por el sistema de fuerzas es igual a la suma geométrica de las aceleraciones impartidas al punto por cada fuerza por separado (Figura 3.1):

Figura 3.1

El concepto de fricción. Tipos de fricción.

Fricción- Resistencia que surge del movimiento de un cuerpo rugoso sobre la superficie de otro. La fricción por deslizamiento resulta en fricción por deslizamiento, y la fricción por rodadura resulta en fricción por balanceo.

Fricción de deslizamiento

Figura 3.2.

La razón es el acoplamiento mecánico de las protuberancias. La fuerza de resistencia al movimiento durante el deslizamiento se denomina fuerza de fricción por deslizamiento (Figura 3.2)

Leyes del rozamiento por deslizamiento:

1. La fuerza de fricción por deslizamiento es directamente proporcional a la fuerza de presión normal:

dondeR- fuerza de presión normal, dirigida perpendicularmente a la superficie de apoyo;F- coeficiente de rozamiento por deslizamiento.

Figura 3.3.

En caso de movimiento del cuerpo plano inclinado(Figura 3.3)

fricción de rodadura

La resistencia a la rodadura está relacionada con la deformación mutua del suelo y la rueda y es mucho menor que la fricción por deslizamiento.

Para un rodamiento uniforme de la rueda, es necesario aplicar fuerzaF dv (Figura 3.4)

La condición de rodadura de la rueda es que el momento de movimiento no debe ser menor que el momento de resistencia:

Figura 3.4.

Ejemplo 1: Ejemplo 2: A dos puntos materiales de masametro 1 = 2 kg ymetro 2 = 5 kg se aplican fuerzas iguales. Compara los valores más rápido.

Solución:

Según el tercer axioma, la dinámica de aceleración es inversamente proporcional a las masas:

Ejemplo 3: Determine el trabajo de la gravedad al mover una carga del punto A al punto C a lo largo de un plano inclinado (Figura 3.7). La fuerza de gravedad del cuerpo es de 1500N. AB=6m, BC=4m. Ejemplo 3: Determine el trabajo de la fuerza de corte en 3 minutos. La velocidad de rotación de la pieza de trabajo es de 120 rpm, el diámetro de la pieza de trabajo es de 40 mm, la fuerza de corte es de 1 kN. (Figura 3.8)

Solución:

1. Trabajar con movimiento rotatorio:

2. Velocidad angular 120 rpm

Figura 3.8.

3. El número de revoluciones para un tiempo dado esz\u003d 120 * 3 \u003d 360 rev.

Ángulo de rotación durante este tiempo φ=2πz\u003d 2 * 3.14 * 360 \u003d 2261 rad

4. Trabajar durante 3 vueltas:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ

Bibliografía

Olofinskaya, V.P. "Mecánica Técnica", Moscú "Foro" 2011

Erdedi A.A. Erdedi N. A. Mecánica teórica. Resistencia de materiales.- R-n-D; Fénix, 2010

dentro de cualquier curso de entrenamiento El estudio de la física comienza con la mecánica. No de la teoría, no de la aplicada y no computacional, sino de la buena mecánica clásica. Esta mecánica también se llama mecánica newtoniana. Según la leyenda, el científico estaba caminando en el jardín, vio caer una manzana, y fue este fenómeno lo que lo impulsó a descubrir la ley de la gravitación universal. Por supuesto, la ley siempre ha existido, y Newton solo le dio una forma comprensible para las personas, pero su mérito no tiene precio. En este artículo, no describiremos las leyes de la mecánica newtoniana con el mayor detalle posible, pero describiremos los conceptos básicos, los conocimientos básicos, las definiciones y las fórmulas que siempre pueden jugar en sus manos.

La mecánica es una rama de la física, ciencia que estudia el movimiento de los cuerpos materiales y las interacciones entre ellos.

La palabra en sí es de origen griego y se traduce como "el arte de construir máquinas". Pero antes de construir máquinas, todavía tenemos un largo camino por recorrer, así que sigamos los pasos de nuestros antepasados y estudiaremos el movimiento de las piedras lanzadas en ángulo hacia el horizonte y las manzanas que caen sobre las cabezas desde una altura h.

¿Por qué el estudio de la física comienza con la mecánica? ¡¿Porque es completamente natural, no partir del equilibrio termodinámico?!

La mecánica es una de las ciencias más antiguas, e históricamente el estudio de la física comenzó precisamente con los fundamentos de la mecánica. Situada en el marco del tiempo y del espacio, la gente, en efecto, no podía partir de otra cosa, por mucho que quisiera. Los cuerpos en movimiento son lo primero a lo que prestamos atención.

¿Qué es el movimiento?

El movimiento mecánico es un cambio en la posición de los cuerpos en el espacio entre sí a lo largo del tiempo.

Es después de esta definición que llegamos naturalmente al concepto de un marco de referencia. Cambiar la posición de los cuerpos en el espacio entre sí. Palabras clave aquí: uno respecto al otro . Después de todo, un pasajero en un automóvil se mueve en relación con una persona parada al costado de la carretera a cierta velocidad, y descansa en relación con su vecino en un asiento cercano, y se mueve a alguna otra velocidad en relación con un pasajero en un automóvil que los supera.

Por eso, para medir normalmente los parámetros de los objetos en movimiento y no confundirnos, necesitamos sistema de referencia - cuerpo de referencia, sistema de coordenadas y reloj rígidamente interconectados. Por ejemplo, la tierra se mueve alrededor del sol en un marco de referencia heliocéntrico. En la vida cotidiana, realizamos casi todas nuestras medidas en un sistema de referencia geocéntrico asociado a la Tierra. La tierra es un cuerpo de referencia con respecto al cual se mueven automóviles, aviones, personas, animales.

La mecánica, como ciencia, tiene su propia tarea. La tarea de la mecánica es conocer la posición del cuerpo en el espacio en cualquier momento. En otras palabras, la mecánica construye una descripción matemática del movimiento y encuentra conexiones entre Cantidades fisicas caracterizándolo.

Para avanzar más, necesitamos la noción de “ punto material ". dicen fisica ciencia exacta, pero los físicos saben cuántas aproximaciones y suposiciones deben hacerse para estar de acuerdo con esta misma precisión. Nadie ha visto nunca un punto material ni olfateado un gas ideal, ¡pero existen! Es mucho más fácil vivir con ellos.

Un punto material es un cuerpo cuyo tamaño y forma pueden despreciarse en el contexto de este problema.

Secciones de mecánica clásica.

La mecánica consta de varias secciones.

Cinemática
Dinámica
Estática

Cinemática desde un punto de vista físico, estudia exactamente cómo se mueve el cuerpo. En otras palabras, esta sección se ocupa de caracteristicas cuantitativas movimiento. Encuentra la velocidad, la ruta - tareas típicas cinemática

Dinámica resuelve la pregunta de por qué se mueve de la forma en que lo hace. Es decir, considera las fuerzas que actúan sobre el cuerpo.

Estática estudia el equilibrio de los cuerpos bajo la acción de las fuerzas, es decir, responde a la pregunta: ¿por qué no cae en absoluto?

Límites de aplicabilidad de la mecánica clásica

mecanica clasica ya no pretende ser una ciencia que lo explica todo (a principios del siglo pasado todo era completamente diferente), y tiene un marco claro de aplicabilidad. En general, las leyes de la mecánica clásica son válidas para el mundo que nos es familiar en términos de tamaño (macromundo). Dejan de funcionar en el caso del mundo de las partículas, cuando se reemplaza el clásico por mecánica cuántica. Además, la mecánica clásica es inaplicable a los casos en que el movimiento de los cuerpos se produce a una velocidad cercana a la de la luz. En tales casos, los efectos relativistas se vuelven pronunciados. En términos generales, en el marco de la mecánica cuántica y relativista - mecánica clásica, este caso especial cuando las dimensiones del cuerpo son grandes y la velocidad es pequeña.

En términos generales, los efectos cuánticos y relativistas nunca desaparecen, también se producen durante el movimiento habitual de los cuerpos macroscópicos a una velocidad muy inferior a la de la luz. Otra cosa es que la acción de estos efectos sea tan pequeña que no pase de las medidas más precisas. La mecánica clásica, por lo tanto, nunca perderá su importancia fundamental.

seguiremos estudiando cimientos físicos mecánica en los siguientes artículos. Para una mejor comprensión de la mecánica, siempre puede consultar nuestros autores, que individualmente arrojan luz sobre el punto oscuro de la tarea más difícil.